Финансовая рента
Например, для годовой ренты при начислении процентов 1 раз в год:
S = A F (T) = A (1 + i) n = ![]() (7)
(7)
Для других видов обычной ренты из (4) и (5), используя множители наращения ![]() и
и ![]() соответственно, получ
соответственно, получ
им:
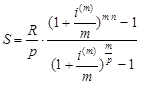 (8)
(8)
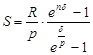 (9)
(9)
В частности, при m = p (период начисления процентов равен периоду ренты) из (4) и (8) получаем
 (10)
(10)
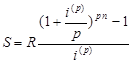 (11)
(11)
Если единицей измерения времени является 1 год, а R - это выплата за год (единицу времени), то множитель в формулах современной стоимости ренты, равный ![]() , называется коэффициентом дисконтирования ренты.
, называется коэффициентом дисконтирования ренты.
Множитель в формулах наращенной суммы ренты, равный ![]() , называется коэффициентом наращения ренты.
, называется коэффициентом наращения ренты.
Из (1) - (11) можно получить коэффициенты наращения и дисконтирования всех рассмотренных видов обычной ренты.
Согласно (1) и (5), коэффициенты дисконтирования и наращения обычной p - срочной ренты с начислением процентов 1 раз в году в течение n лет равны соответственно:
 (12)
(12)
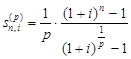 (13)
(13)
![]() и
и ![]() - это соответственно современная стоимость и наращенная сумма постоянной обычной p - срочной ренты с ежегодной выплатой 1 д. е. равными долями p раз в году в размере
- это соответственно современная стоимость и наращенная сумма постоянной обычной p - срочной ренты с ежегодной выплатой 1 д. е. равными долями p раз в году в размере ![]() в моменты времени
в моменты времени ![]() с начислением на члены ренты процентов 1 раз в году.
с начислением на члены ренты процентов 1 раз в году.
Следовательно, ![]() и
и ![]() связаны соотношением (14):
связаны соотношением (14):
![]() = (1 + i) n
= (1 + i) n![]() (14)
(14)
Аналогичный смысл имеют коэффициенты дисконтирования и наращения других рассмотренных видов обычной ренты.
Для этих рент имеем соотношения:
![]() - годовая рента с начислением процентов 1 раз в год;
- годовая рента с начислением процентов 1 раз в год;
![]() - p - срочная рента с начислением процентов m раз в год;
- p - срочная рента с начислением процентов m раз в год;
![]() - p - срочная рента с непрерывным начислением процентов.
- p - срочная рента с непрерывным начислением процентов.
Коэффициенты дисконтирования и наращения годовой ренты при начислении процентов 1 раз в год:
![]() и
и ![]() (15)
(15)
Если применяется p - срочная рента с начислением процентов p раз в год (m = p) по годовой номинальной ставке i (p), то за единицу измерения времени можно принять ![]() часть года. Тогда
часть года. Тогда ![]() - выплата за единицу времени (постнумерандо),
- выплата за единицу времени (постнумерандо), ![]() - процентная ставка за 1 единицу времени,
- процентная ставка за 1 единицу времени,
срок ренты - np единиц времени.
Коэффициенты дисконтирования и наращения такой ренты равны соответственно
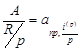 и
и 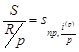 .
.
Из формул (10), (11) имеем
 ,
,  (16),
(16),
что позволяет для этой ренты использовать те же таблицы коэффициентов. Заметим, что если единицей измерения времени является 1 год, то коэффициенты дисконтирования и наращения этой ренты определяются как ![]() =
= ![]() и
и ![]() =
= ![]() и рассчитываются по формулам, полученным из (10), (11):
и рассчитываются по формулам, полученным из (10), (11):
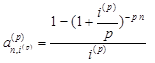 ,
,  (17). Тогда
(17). Тогда
![]() =
= ![]() и
и ![]() =
= ![]() (18)
(18)
Рассмотрим ренту пренумерандо.
Связь между коэффициентами дисконтирования и наращения рент пренумерандо и постнумерандо следует из их определения. Срок дисконтирования каждого платежа ренты пренумерандо уменьшается, а срок наращения увеличивается на один период ренты по сравнению с обычной рентой. По - прежнему единицей измерения времени считаем 1 год. Если ![]() и
и ![]() - коэффициенты дисконтирования и наращения p - срочной ренты пренумерандо (платежи поступают в начале каждого периода длиной
- коэффициенты дисконтирования и наращения p - срочной ренты пренумерандо (платежи поступают в начале каждого периода длиной ![]() ) при начислении на члены ренты процентов 1 раз в год, то справедливы соотношения:
) при начислении на члены ренты процентов 1 раз в год, то справедливы соотношения:
![]() =
= ![]()
![]()
![]() =
= ![]()
![]()
![]() = (1 + i) n
= (1 + i) n ![]() .
.
Отсюда при p = 1 получаем соотношения для годовых рент:
![]() =
= ![]()
![]()
![]() =
= ![]()
![]()
![]() = (1 + i) n
= (1 + i) n ![]() .
.
При непрерывном начислении процентов для p - срочной ренты имеем соотношения:
Другие рефераты на тему «Экономико-математическое моделирование»:
Поиск рефератов
Последние рефераты раздела
- Выборочные исследования в эконометрике
- Временные характеристики и функция времени. Графическое представление частотных характеристик
- Автоматизированный априорный анализ статистической совокупности в среде MS Excel
- Биматричные игры. Поиск равновесных ситуаций
- Анализ рядов распределения
- Анализ состояния финансовых рынков на основе методов нелинейной динамики
- Безработица - основные определения и измерение. Потоки, запасы, утечки, инъекции в модели
