Сетевое планирование и управление. Основы регрессионного анализа

Событие обозначается кружком, который содержит следующую информацию:

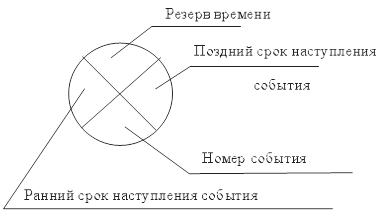
Номер исходного события равен единице. Номера остальных событий соответствуют последней цифре кода предшествующей данному событию работы (или работ).

При построении сетевого графика должна соблюдаться существующая очерёдность выполнения работ.

Д

ля определения средних значений резервов времени по отдельным событиям определяются средние значения ранних и поздних сроков событий начала и окончания работ.

Путём в сетевом графике называется любая последовательность работ (стрелок), связывающая какие-либо два события. При этом пути, связывающие исходное и завершающее события сети, считаются полными, а все другие пути – неполными. Каждый путь характеризуется своей продолжительностью (длительностью), которая равна сумме продолжительностей составляющих его работ.

Наиболее простым и наглядным методом расчёта параметров сети является графический. Кружки-события заполняются в следующем порядке:

В нижний сектор ставится порядковый номер события.

Путём последовательного перехода от исходного события, ранний срок свершения которого равен нулю, к завершающему событию рассчитываются ранние сроки его свершения. Ранний срок наступления события представляет собой минимальный из возможных моментов наступления должного события при заданной продолжительности работ и начальном моменте.

Ранний срок наступления j-го события вычисляется по формуле:

, i =1,…,к,

где (i =1,…,к) – ранний срок наступления i-го события;

(i =1,…,к) – средняя продолжительность работы ij;

к – число работ, непосредственно предшествующих j-му событию.

Ранние сроки определяются величиной наиболее длительного отрезка пути от исходного события до рассматриваемого.

Путём последовательного перехода от завершающего события, поздний срок которого равен величине критического пути, рассчитывают поздний срок его свершения. Этот срок определяется разностью продолжительности критического пути и максимальным из путей, следующим за этим событием.

, j =1,…,,

где (j=1,…,) – поздний срок наступления j-го события;

– число работ, непосредственно следующих за i-м событием (все эти работы на сетевом графике обозначаются стрелками, выходящими из кружка, обозначающего i-ое событие).

Поздний срок наступления завершающего события принимается равным раннему сроку наступления того же события.

Разность между поздним и ранним сроками свершения событий – есть резерв времени этого события. Резерв времени i-го события вычисляется по формуле:

.

После вычисления резервов времени определяется критический путь , то есть полный путь, имеющий наибольшую продолжительность. Для него является характерным, что все события, принадлежащие ему, не имеют резервов времени (они равны нулю).

Полный резерв времени работы, представляющий собой максимальное время, на которое можно увеличить продолжительность работы (не изменяя длительности критического пути), определяется как разность между поздним сроком свершения события, завершающего работу, и ранним сроком свершения предшествующего работе события минус продолжительность самой работы.

1.4 Решение типовой задачи

На предприятии осуществляется реконструкция цеха. Известна средняя продолжительность выполнения отдельных работ (таблица 1.1). Среднеквадратическое отклонение продолжительности выполнения работ по всем работам равно одному дню.

Необходимо:

1. Построить сетевой график по выполнению работ по реконструкции цеха и определить значение его параметров (ранние и поздние сроки наступления событий, начала и окончания работ, резервы времени по отдельным событиям).

2. Определить на сетевом графике критический путь, дать перечень работ, принадлежащих к критическому пути и его длительность. На сетевом графике выделить критический путь.

Таблица 1.1

Определяем ранние сроки наступления j-го события сетевого графика:

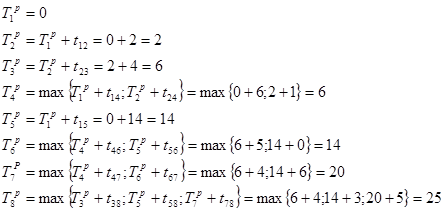
Определяем поздние сроки свершения i- го события :

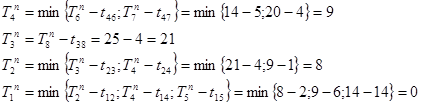
Определим резерв времени i-го события сетевого графика.

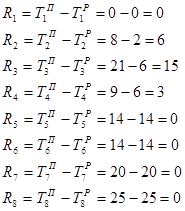
Определим критический путь сетевого графика , т.е. полный путь, имеющий наибольшую продолжительность и характеризующийся тем, что все принадлежности ему события не имеют резервов времени (они равны нулю).

Рассмотрим все пути, проходящие через вершины сетевого графика с нулевыми резервами времени:

 Скачать реферат