Решения задачи планирования производства симплекс методом

14 - разрешающий элемент каждой таблицы, 15 - переход от старого базиса к новому, 16 - количество итераций, 17 - информация об оптимальности решения, 18 – Ответ, в нашем случае максимум целевой функции (максимальная прибыль), 19 – оптимальный набор производимой продукции (количество изделий A,…,E). (см. Рис.11)

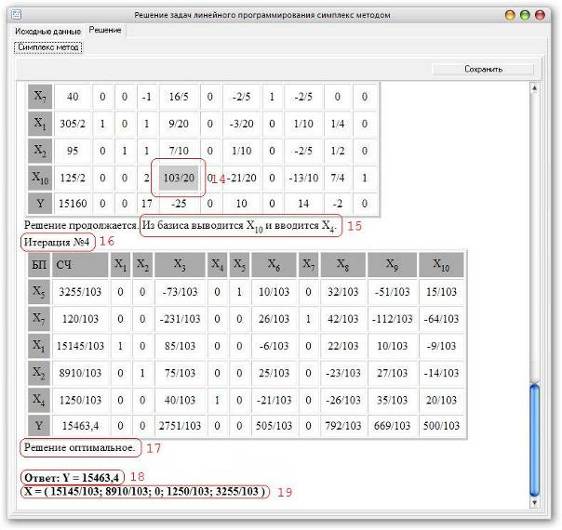
Рис.11 Работа с программой

4.4 Схема программы

Логическая структура программы решающей задачи ЛП симплекс методом приведена на Рис.12, Рис.13, Рис.14.

Рис.12 Симплекс метод

Рис.13 Поиск r-столбца

Рис.14 Поиск s-строки

Заключение

Развитие современного общества характеризуется повышением технического уровня, усложнением организационной структуры производства, углублением общественного разделения труда, предъявлением высоких требований к методам планирования производственной деятельности. В этих условиях только научный подход к экономике предприятий позволит обеспечить высокие темпы развития промышленности. Научного подхода требует и решение тактических и стратегических задач.

В настоящее время новейшие достижения математики и современной вычислительной техники находят все более широкое применение как в экономических исследованиях и планировании, так и в других задачах. Этому способствует развитие таких разделов математики как математическое программирование, теория игр, теория массового обслуживания, а также бурное развитие быстродействующей электронно-вычислительной техники.

Уже накоплен большой опыт постановки и решения экономических и тактических задач с помощью математических методов. Особенно успешно развиваются методы оптимального управления. Экономика и производство развивается быстро там, где широко используются математические методы.

Список литературы

1. Схрейвер А. Теория линейного и целочисленного программирования: в 2-х т. Т.2: Пер с англ. - М.: Мир, 1991. - 342с., ил. Раздел Целочисленное линейное программирование

2. Конюховский П.В. Математические методы исследования операций в экономике. - СПб: Питер, 2002. - 208 с.: ил. - (Серия "Краткий курс"). Раздел 4.2 Метод Гомори

3. Хемди А. Таха Глава 3. Симплекс-метод // Введение в исследование операций = Operations Research: An Introduction. — 7-е изд. — М.: «Вильямс», 2007. — С. 95-141. — ISBN 0-13-032374-8

4. Томас Х. Кормен и др. Глава 29. Линейное программирование // Алгоритмы: построение и анализ = INTRODUCTION TO ALGORITHMS. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1

5. Ершов А.Т., Карандаев И.С., Шананин Н.А. Планирование производства и линейное программирование. МИУ, М., 1981.

6. Акулич И.Л., «Математическое программирование в примерах и задачах», Москва «Высшая школа» 1993г.

7. Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. «Математическое программирование», Москва «Высшая школа» 1980г.

8. Вентцель Е.С. Исследование операций: задачи, принципы, методологии. М.: Изд-во «Наука», 1980.

9. Джерод Холлингворс, Дэн Баттерфилд, Боб Свот C++ Builder 5. Руководство разработчика = C++ Builder 5 Developer's Guide. — М.: «Диалектика», 2001. — С. 884. — ISBN 0-672-31972-1

10. Джаррод Холингворт, Боб Сворт, Марк Кэшмэн, Поль Густавсон Borland C++ Builder 6. Руководство разработчика = Borland C++ Builder 6 Developer's Guide. — М.: «Вильямс», 2004. — С. 976. — ISBN 0-672-32480-6

11. Леоненков А.В. Решение задач оптимизации в среде MS Excel BHV-Санкт-Петербург ISBN: 5941575033 2005 г.

Приложение 1

Листинг программы

// Этот файл определяет класс симплекс метода

#include <vcl.h>

#include <list>

#include "CD.cpp"

#ifndef CSM2_H

#define CSM2_H

namespace SM

{

//----------------Симплекс метод------------------------------

class CSM

{

public:

CSM( int n, int m );

void SetBaz( int * baz );

int SetT( CD ** T );

void Show();

AnsiString GetWord();

AnsiString GetTacker();

AnsiString Get_Rap();

int operator<<=( CSM * csm );

CD get_CF();

CD** get_ogr(){ return T; }

int* get_baz(){ return baz; }

int get_rez(){ return rez; }

void get_nm( int* nIn, int* mIn ){ *nIn = n; *mIn = m; }

void get_ij( int* i, int* j ){ *i = a_i; *j = a_j; }

~CSM( );

private:

static int iter; // Число итераций

int optim(); // проверка решение (0 - оптимальное, 1 - не существует, 2 - не оптимальное)

int n; // Число переменных

int m; // Число ограничений

int a_i;

int a_j; // Координаты разрешающего элемента

int * baz; // Массив базисных переменных

CD ** T; // Симплекс таблица

int rez;

};

int CSM::iter = 0; // Число итераций

CSM::CSM( int nIn, int mIn )

{

n = nIn;

m = mIn;

baz = new int [m];

T = new CD * [m + 1]; // m + 1 т.к. еще строка целевой функции

for( int i = 0; i < m + 1; i++ )

T[i] = new CD [n + 1]; // n + 1 т.к. еще свободный член

iter += 1;

rez = 2;

}

CSM::~CSM( )

{

delete baz;

for( int i = 0; i < m + 1; i++ )

delete T[i];

delete T;

iter -= 1;

}

void CSM::SetBaz( int * bazIn )

{

for( int i = 0; i < m; i++ )

baz[i] = bazIn[i];

}

int CSM::SetT( CD ** TIn ) // Копирование входящей таблицы и проверка решения с поиском разрешающего элемента

{

for( int i = 0; i < m + 1; i++ )

for( int j = 0; j < n + 1; j++ )

T[i][j] = TIn[i][j];

return optim();

}

int CSM::optim()

{

a_i = a_j = 0; // Инициализация координат разрешающего элемента

// Проверка на отрицательность среди свободных членов

for( int i = 1; i < m; i++ ) // проверка свободного члена

if( T[i][0].get_d() < T[a_i][0].get_d() ) // Ищем минимальный

a_i = i;

if( T[a_i][0].get_d() < 0 ) // Если минимальный элемент отрицательный (двойственный СМ)

{

for( int j = 1; j < n + 1; j++ ) // проверка на наличие отрицательных эл-тов в строке

if( T[a_i][j].get_d() < 0 ) // есть отрицательные элементы

{

a_j = j; // Первый отрицательный элемент

break; // Выход из цикла поиска

}

if( a_j == 0 ) return rez = 1; // Нет оптимального решения // выход

for( int j = a_j + 1; j < n + 1; j++ ) // Проходим по строке еще раз для нахождения минимального отношения

if( T[a_i][j].get_d() < 0 ) // Отрицательный

if( fabs( (T[m][j]/T[a_i][j]).get_d() ) < fabs( (T[m][a_j]/T[a_i][a_j]).get_d() ) ) // Наименьшее отношение

a_j = j;

return rez = 2; // продолжение выполнений итераций // выход

}

// Проверка на отрицательность среди элементов целевой функции

a_j = 1;

a_i = m;

for( int j = 2; j < n + 1; j++ ) // Проходим по строке целевой функции

if( T[m][j].get_d() < T[m][a_j].get_d() ) // Ищем минимальный

 Скачать реферат