Экономико–математическое моделирование на железнодорожном транспорте
9. FN. PF – PN = 15-12=3; CFN = 10; нарушений нет.
10.GF. PG – PF = 15-15=0; CGF = 11; нарушений нет.
11.GC. PG– PC = 15-3=12; CGC = 12; нарушений нет.
Корректировка плана:
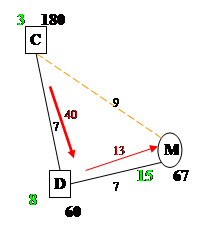
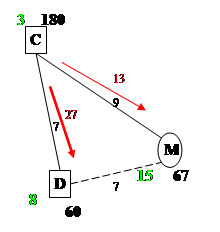
Построение системы потенциалов, проверка плана на оптимальность:
1. AJ. PA – PJ = 10-5=5; CAJ = 8; нарушений нет.
2. GN. PG – PN = 15-12=3; CGN = 12; нарушений нет.
3. GH. PG – PH = 15-12=3; CGH = 16; нарушений нет.
4. HC. PH – PC = 12-3=9; CHC = 12; нарушений нет.
5. LE. PL – PE = 26-6=20; CLE = 12; нарушение составит 20 единиц.
6. MD. PM – PD = 15-8=7; CMC =7; нарушений нет.
7. KE. PK – PE = 16-9=8; CEK = 14; нарушений нет.
8. KN. PK – PN = 16-12=4; CKN = 21; нарушений нет.
9. FN. PF – PN = 15-12=3; CFN = 10; нарушений нет.
10.GF. PG – PF = 15-15=0; CGF = 11; нарушений нет.
11.GC. PG– PC = 15-3=12; CGC = 12; нарушений нет.
Корректировка плана:
Построение системы потенциалов, проверка плана на оптимальность:
1. AJ. PA – PJ = 10-5=5; CAJ = 8; нарушений нет.
2. GN. PG – PN = 15-12=3; CGN = 12; нарушений нет.
3. GH. PG – PH = 15-12=3; CGH = 16; нарушений нет.
4. HC. PH – PC = 12-3=9; CHC = 12; нарушений нет.
5. LM. PL – PM = 26-14=12; CLE = 12; нарушений нет.
6. MD. PM – PD = 15-8=7; CMC =7; нарушений нет.
7. KE. PK – PE = 16-9=8; CEK = 14; нарушений нет.
8. KN. PK – PN = 16-12=4; CKN = 21; нарушений нет.
9. FN. PF – PN = 15-12=3; CFN = 10; нарушений нет.
10.GF. PG – PF = 15-15=0; CGF = 11; нарушений нет.
11.GC. PG– PC = 15-3=12; CGC = 12; нарушений нет.
F4=3*15+87*16+31*14+10*44+26*12+13*9+48*4+17*3+50*5+39*12+120*9= 4781
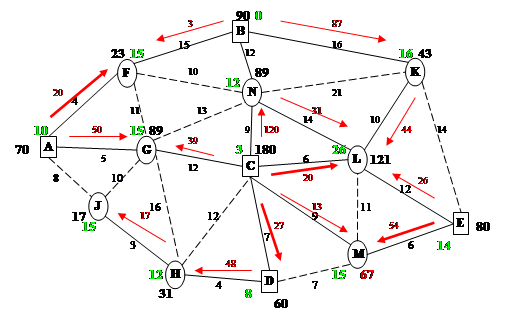
Рассмотрим наш план. Поставщик А по оптимальному плану должен обеспечивать спрос потребителей F,G. Поставщик B по оптимальному плану должен обеспечивать спрос потребителей F,K. Поставщик C по оптимальному плану должен обеспечивать спрос потребителей G,N,L,D. Поставщик D по оптимальному плану должен обеспечивать спрос потребителя M. Поставщик E по оптимальному плану должен обеспечивать спрос потребителей H,M.
Рассчитаем целевую функцию оптимального плана:
Получен эффект от оптимизации: F3-F4 =6010 – 4781=1229
Рассчитаем прокатную оценку: 1) 20-26+54-13=35 2)54-13+20-26=35 3)20- 3+87+44-26+54-13+39-50=152
2 Обобщенная транспортная задача
Имеется возможность выпуска 5 видов продукции (j=1, j=2, j=3, j=4, j=5) на трех типах оборудования (i=1, i=2, i=3).
1. Сформировать математическое описание задачи
2. Построить первоначальное распределение
3. Найти оптимальный план модифицированным методом потенциалов
4. Выполнить анализ оптимального производственного плана, включая состав и объем выпуска продукции, и состояние использованных ресурсов.
Математическая модель распределительной транспортной задачи состоит в следующем:
Найти:
При Здесь:
1. i – индекс ресурсов;
2. j – индекс производимой продукции, работы, выполняемых перевозок;
3. xij - неизвестное, характеризующее объем ;
4. kij – производительность ресурсов при выполнении работы j;
5. сij – расходы (себестоимость) при выполнении работы с привлечением ресурсов i;
6. ai – ресурсы с номером i;
7. bi –потребность в работе с номером j;
1. Согласно номеру варианта курсовой работы:
В верхнем левом углу ячеек введем значение показателей
производительности ресурсов(машин например) при выполнении работы (kij).
В нижнем правом углу каждой из ячеек введем значение расходов при выполнении работы с привлечением ресурсов i(т.е. себестоимости единицы выпущенной продукции). Красным в клетках справа обозначим данные по ресурсам оборудования, зеленым снизу – данные по потребности выпуска продукции.
Расстановка потенциалов начинается с третьей строки, имеющей резерв неиспользованных ресурсов. Такой строке присваивается потенциал:
U3=0.Остальные потенциалы находим по формулам:
При выполнении проверки решения на оптимальность применяем следующее условие: 2. Анализ полученного оптимального производственного плана.
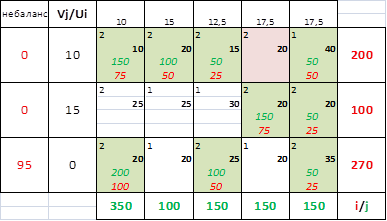
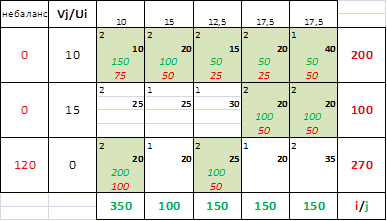
Целевая функция оптимального плана составляет:
F=150*10+100*20+50*15+50*20+50*40+100*20+100*20+200*20+100*25=17750 условных единиц расходов.
В соответствии с планом первые пять видов продукции выполняются с помощью первого ресурса, который полностью израсходован. Четвертый и пятый виды продукции производятся с помощью второго ресурса, который полностью израсходован. Первый и третий ресурсы используются не полностью и остаток их составляет 120 ед. Наиболее эффективно используется второй ресурс. Его потенциал составляет 15 ед. Первый вид ресурсов используется менее эффективно(потенциал = 10 ед.). Раз потенциал третьего ресурса равен нулю, это означает что он используется не полностью. Потенциалы столбцов в распределительных транспортных задачах выполняют роль индикаторов эффективности производства. Чем меньше потенциал, тем эффективнее производится продукция, и, наоборот. В оптимальном плане с наименьшей себестоимостью и производительностью вырабатывается первый продукт с испоьзованием первого ресурса. Соответствующий потенциал
V1=10. Менее выгодно по сравнению с первым производство 3 -его, 2-го и 5,4-го изделий, где V3= 12,5; V2= 15; V4= V5==17,5.
3 Применение методов математической статистики в экономических расчетах
3.1 Расчет параметров регрессионных моделей. Проверка надежности найденных статистических показателей и вариации изменений
1. Установить статистическую зависимость между годовым оъемом работы по грузообороту (млрд. ткм), приняв ее за независимую переменную (x) и фондоемкостью перевозок приняв ее за независимую переменную (Y). Составить линейную модель вида Y = a + b*x, где a= y*-b*x*, 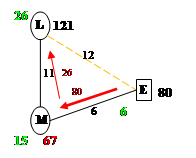
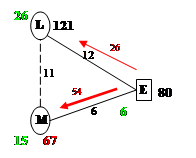
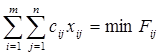
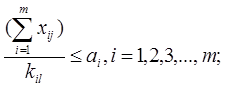
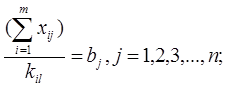
![]()

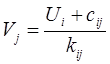
![]()
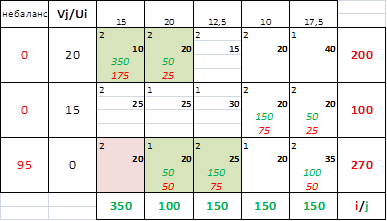
![]() и помечаем клетку где условие оптимальности не выполняется. Оптимизируем план.
и помечаем клетку где условие оптимальности не выполняется. Оптимизируем план.
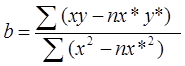 .
.
Другие рефераты на тему «Экономико-математическое моделирование»:
Поиск рефератов
Последние рефераты раздела
