Экономико–математическое моделирование на железнодорожном транспорте

План

1 Использование методов линейного программирования для целей оптимального распределения ресурсов

1.1 Оптимизация плана перевозок с использованием метода потенциалов

1.2 Оптимизация плана ТЗ с использованием метода потенциалов на сети

2 Обобщенная транспортная задача

3 Применение методов математической статистики в экономических расчетах

3.1 Расчет параметро

в регрессионных моделей. Проверка надежности найденных статистических показателей и вариации изменений

3.2 Расчет параметров парной корреляции

3.3 Выравнивание рядов распределений с проверкой гипотезы нормальности по критерию Пирсона на базе эмпирического ряда величин себестоимости железнодорожной перевозки

4 Прогнозирование экономических показателей методом простого экспоненциального сглаживания

5 Математические функции финансового менеджмента

5.1 Расчет функции регулярного платежа Payment (PMT)

5.2 Расчет функции срока накопления TERM при регулярном платеже

5.3 Расчет функции срока накопления CTERM

5.4 Расчет функции FV при регулярном платеже PMT

5.5 Расчет функции приведения капитала к настоящему времени (PV) при регулярных инвестициях (PMT)

5.6 Расчет ставки банковского процента RATE

5.7 Расчет функции денежных потоков

5.8 Расчет функции внутреннего уровня доходности (IRR)

Список литературы

1 Использование методов линейного программирования для целей оптимального распределения ресурсов

1.1 Оптимизация плана перевозок с использованием метода потенциалов

1. Составим допустимый план транспортной задачи, используя метод минимальной стоимости или Мюллера – Мербаха для построения базисного плана с ограничениями пропускной способности.

2. Найти оптимальный план транспортной задачи, используя метод потенциалов. Построенный допустимый и оптимальный план должен удовлетворять условиям постановки транспортной задачи.:

a.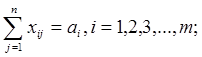

b.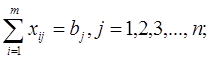

c.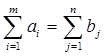

d. 0≤xij≤dij

e. Целевая функция задачи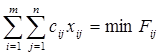

3. Рассчитать целевые функции каждого базисного плана перевозок

4. Найти экономический эффект от оптимизации. Экономический эффект от оптимизации рассчитывается как разность между целевыми функциями базисного и оптимального планов.

5. Рассчитать матрицу показателей характеристик оптимального плана перевозок транспортной задачи. Характеристики клеток рассчитываются по формуле: Dij = cij – (Vi – Uj)

6. Показать варианты альтернативных решений при одной и той же целевой функции и при минимальных от нее отклонениях.

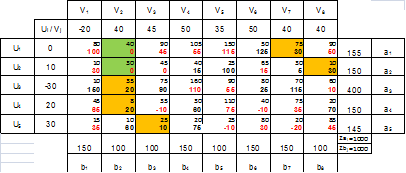
1. Составим допустимый план транспортной задачи, используя метод минимальной стоимости для построения базисного плана с ограничениями пропускной способности.

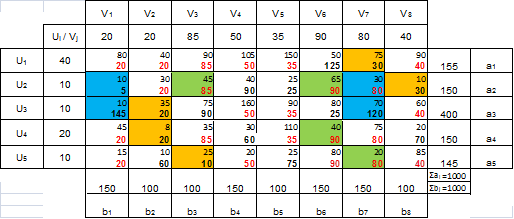
Исходные данные:

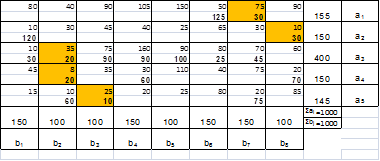
Рассчитаем целевую функцию базисного плана перевозок: F1= 52010

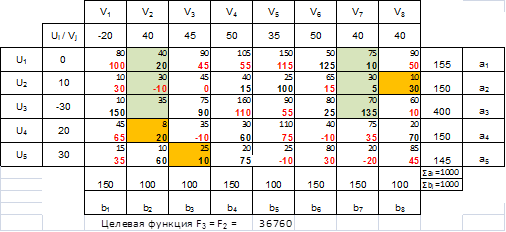
2. Найдем оптимальный план транспортной задачи, используя метод потенциалов.

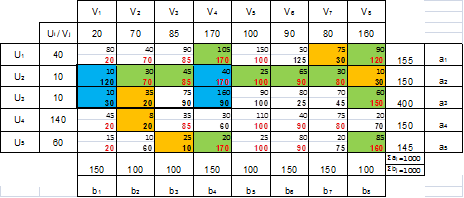
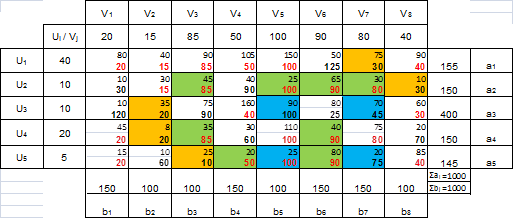
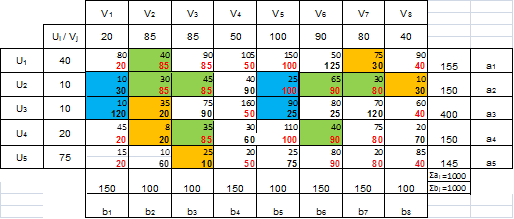
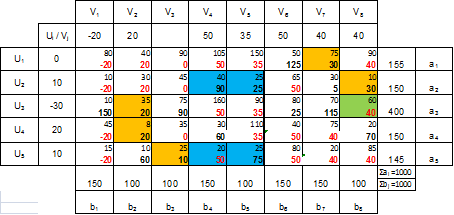
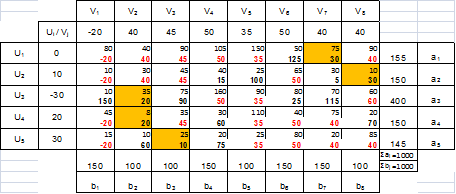
Найден оптимальный план (согласно условиям а – е пункта 2 на стр. 3). Рассчитаем целевую функцию плана. F2 = 36760

4. Экономический эффект от оптимизации: F2- F1 = 52010-36760 = 15250

5. Рассчитаем матрицу показателей характеристик оптимального плана перевозок транспортной задачи.

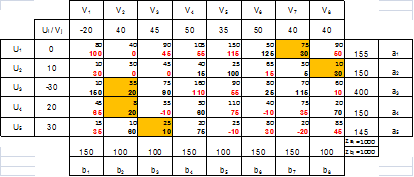
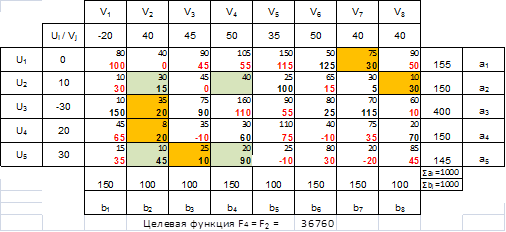
6. Покажем варианты альтернативных решений при одной и той же целевой функции и при минимальных от нее отклонениях:

1.2 Оптимизация плана ТЗ с использованием метода потенциалов на сети

1. Найти оптимальный план транспортной задачи, используя метод потенциалов

2. Рассчитать целевые функции оптимального плана перевозок

3. Найти экономический эффект от оптимизации.

4. Рассчитать прокатные оценки для небазисных звеньев с ограничением пропускной способности.

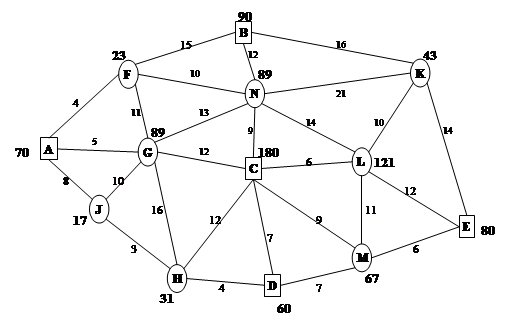
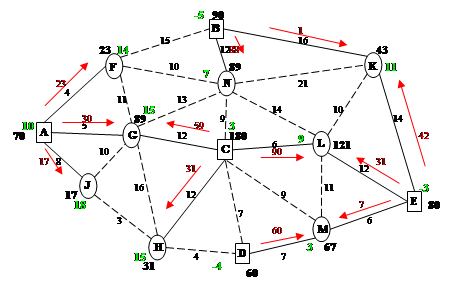
Построение допустимого плана:

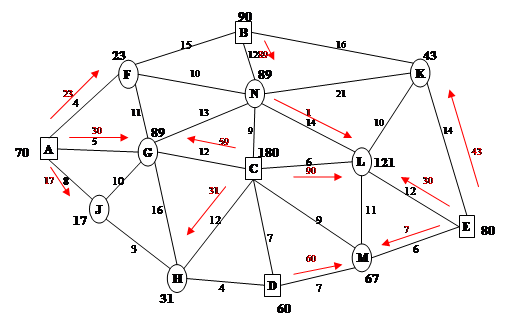
Рассчитаем функцию цели

:F1=23*4+43*14+7*6+60*7+17*8+30*5+89*12+30*12+31*12+59*12+14+90*6 = 4504

Количество потоков в базисном плане = 12.

Расстановка потенциалов:

Присвоим узлу А потенциал равный 10. Найдем потенциалы соседних вершин по базисным звеньям.

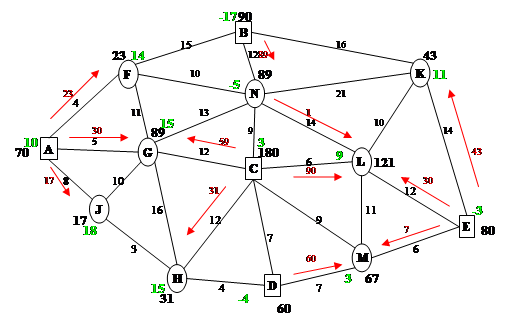
Проверка плана на оптимальность:

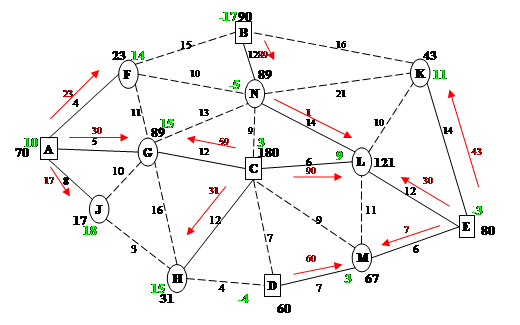
Рассмотрим все небазисные звенья: (обозначим их на рисунке пунктиром)

1. JH. PJ – PH = 18-15=3; CFB = 3; нарушений нет.

2. JG. PJ – PG = 18-15=3; CJC = 10; нарушений нет.

3. GH. PG – PH = 15-15=0; CGH = 16; нарушений нет.

4. HD. PH – PD = 15+4=19; CHD = 4; нарушение составит 19-4=15.

5. CD. PC – PD = 3+4=7; CCD = 7; нарушений нет.

6. CM. PC – PM = 3-3=0; CCM = 9; нарушений нет.

7. LM. PL – PM = 9-3=6; CLM = 11; нарушений нет.

8. KL. PK – PL = 11-9=2; CKL = 10; нарушений нет.

9. KN. PK – PN = 11+5=15; CKN = 21; нарушений нет.

10.KB. PK – PB = 11+17=28; CKB = 16; нарушение составит 28-16=12.

11.FB. PF – PB = 14+17=31; CFB = 16; нарушение составит 31-16=15.

12.FN. PF – PN = 14+5=19; CFN = 10; нарушение составит 19-10=9.

13.GF. PG – PF = 15-14=1; CGF = 11; нарушений нет.

14.CN. PC – PN = 5+3=8; CCN = 9; нарушений нет.

15.GC. PG – PC = 15-3=12; CGC = 12; нарушений нет.

Корректировка плана:

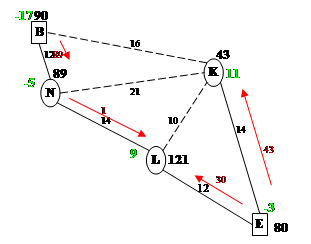
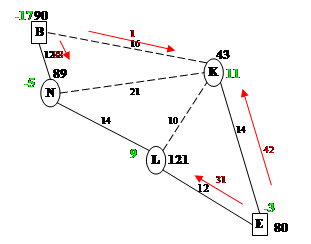
Построение системы потенциалов, проверка плана на оптимальность:

Рассмотрим все небазисные звенья: (обозначим их на рисунке пунктиром)

1. JH. PJ – PH = 18-15=3; CFB = 3; нарушений нет.

2. JG. PJ – PG = 18-15=3; CJC = 10; нарушений нет.

 Скачать реферат