Экономико–математическое моделирование на железнодорожном транспорте

2. Определить достоверность найденного уравнения регрессионной модели, используя критерий Фишера. Для использования критерия Фишера (F) устанавливается отношение (h) полной дисперсии (s^2y) к остаточной(s^2y,x): 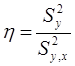; ;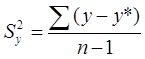rc="images/referats/9805/image063.png">

m – число факторов модели (m=2), n – число испытаний, n = 12.

В

соответствующей статистической таблице F - распределения определим, что с доверительной вероятностью, например, в 95 случаях из 100 мы имеем удовлетворительный результат, так как f(0.95)= 2.94, и меньше значения

. Полученный результат позволит нам использовать рассчитанное уравнение регрессии для различных целей, включая прогнозирование.

3.2 Расчет параметров парной корреляции

3. Найти значение коэффициента корреляции для проверки статистической зависимости между годовым объемом работы по грузообороту (млрд. ткм), (х) и фондоемкостью перевозок (у) по данным варианта.

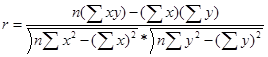
Определить значимость найденного в задании 3 коэффициента корреляции. Сделать вывод о доверительности найденных значений, используя таблицу нижних границ значимости коэффициента корреляции с уровнем значимости 0,95. Вывод о значимости найденного значения линейного коэффициента корреляции в 95 случаях из 100 принимается при условии, что он больше соответствующей нижней границы.

Используя таблицу нижних границ значимости коэффициента корреляции с уровнем значимости 0,95 делаем вывод о доверительности найденных значений и значимости найденного значения линейного коэффициента корреляции в 95 случаях из 100.

3.3 Выравнивание рядов распределений с проверкой гипотезы нормальности по критерию Пирсона на базе эмпирического ряда величин себестоимости железнодорожной перевозки

Требуется подтвердить гипотезу нормальности распределения эмпирического ряда величин себестоимости пропуска транзитных вагонов по участкам железных дорог и найти теоретическое нормальное распределение этих величин. Для этого необходимо найти величину расхождения между указанными распределениями, используя критерий Пирсона.

Среднее значение ряда рассчитывается по формуле:

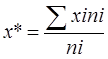
Среднеквадратическое отклонение рассчитывается по формуле:

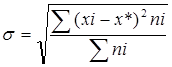
Нормированное отклонение рассчитывается по формуле:

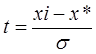
Функция плотности вероятности:

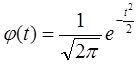
fi =φ(t)*y

Значение величины эмпирического нормированного отклонения:

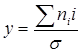
Критерий Пирсона:

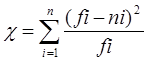
Число степеней свободы r = k-3, где k – число интервалов в фактическом распределении.

Поскольку найденное значение в расчете «хи-квадрат» больше табличного, гипотеза о соответствии эмпирического распределения теоретическому не принимается

.

4 Прогнозирование экономических показателей методом простого экспоненциального сглаживания

Рассчитать заданным методом прогноз для локомотивного депо на 10 – й год при параметрах сглаживания α = 0,3 и α = 0,5. Выполним данное задание,используя пакет «Анализ данных » MS Excel.

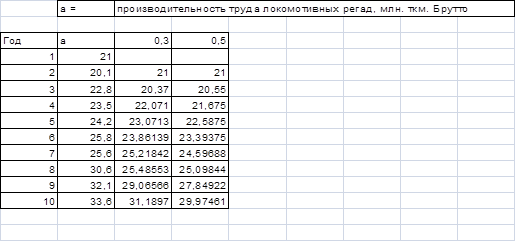
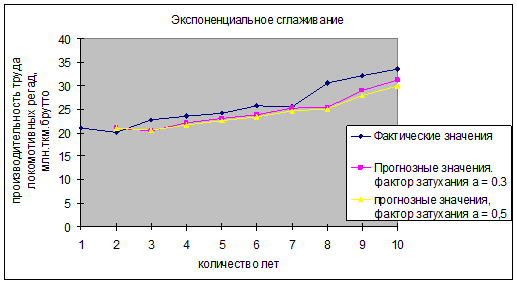
5 Математические функции финансового менеджмента

5.1 Расчет функции регулярного платежа Payment (PMT)

Выполнить следующие расчеты по номеру варианта:

1. Расчет функции регулярного платежа Payment (PMT).

2. Рассчитать функцию платежа, если срок кредита удвоится.

3. Как изменится функция РМТ, если размер процента по банковскому кредиту увеличится на 10% по первому пункту задания.

4. Как изменится функция РМТ, если размер процента по банковскому кредиту увеличиться на 10 % по второму пункту задания.

Среди функций с регулярными выплатами наиболее часто применяется функции регулярного платежа Payment или сокращенно РМТ в случае обслуживания займов, кредитов и в других операциях.

Предположим нами взят кредит на приобретение оборудования, рассчитать размер PMT - ежемесячных платежей по возврату кредита, если известен размер кредита - наш основной капитал - Principal - (Prin), размер ставки банковского процента (i), под который был взят кредит и срок отдачи ссуды (n), который может исчисляться в месяцах или годах. Если срок отдачи кредита задан в месяцах, расчет выполняется по формуле:

,

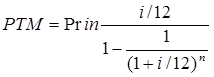где Prin – размер кредита; i – размер ставки банковского процент; n – срок отдачи ссуды.

Ставка кредита в этой формуле задается в десятичных дробях.

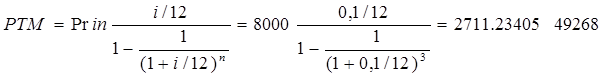
1. Если срок кредита удваивается:

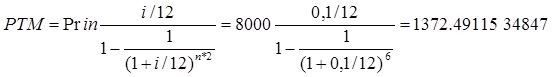
2. Если размер процента по банковскому кредиту увеличиться на 10 % по первому пункту задания:

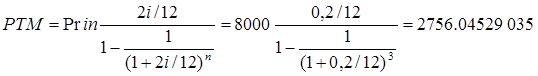
3. Если размер процента по банковскому кредиту увеличиться на 10 % по второму пункту задания:

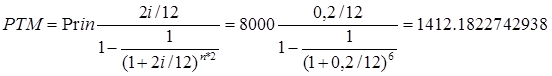
5.2 Расчет функции срока накопления TERM при регулярном платеже

По своему варианту выполнить следующие расчеты:

1. Рассчитать функцию TERM.

2. Рассчитать функцию TERM, если PMT удвоится

3. Как изменится функция TERM, если размер процента по банковскому кредиту увеличиться на 10 % по первому пункту задания.

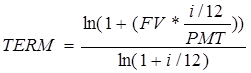
1.

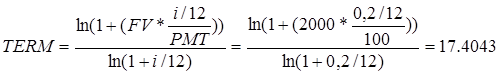
2.

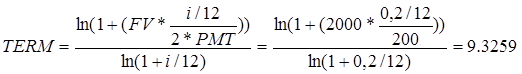
3.

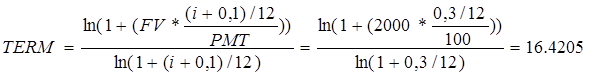
5.3 Расчет функции срока накопления CTERM

По своему варианту выполнить следующие расчеты:

1. Рассчитать функцию СTERM.

2. Рассчитать функцию СTERM, если размер процента по банковскому кредиту уменьшаться на 20 %. по первому пункту задания.

 Скачать реферат