Моделирование и прогнозирование цен на бензин 2007

На основе исходных данных, представленных в таблице Приложения 1, можно построить гистограмму и график на нормальной вероятностной бумаге для исследуемого показателя Yt.

По гистограмме и графику на нормальной вероятностной бумаге видно, что распределение величины Yt относительно близко к нормальному закону. (см. Приложение 2).

По диаграмме рассеивания видно, что можно построить такую прямую, которая бы описывала имеющуюся тенденцию цен к повышению, т.е. распределение Yt не случайно. Следовательно, результирующий показатель Yt имеет прямую функциональную зависимость от времени, а значит, необходимо проверить его на автокорреляцию уровней временного ряда. Для этого вычисляются коэффициенты автокорреляции. Величина максимального лага определяется по формуле , где Т- объем выборки. Следовательно, .

Коррелограмма имеет вид:

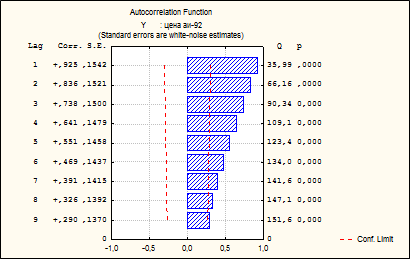
Все коэффициенты автокорреляции положительны и постепенно снижаются Следовательно, можно сделать вывод о том, что в ряду наблюдается долгосрочная тенденция, для такого ряда лучше всего подходит трендовая модель вида

2.2. Построение трендовой модели. Прогнозирование при помощи трендовой модели.

Для исследуемого временного ряда Y можно подобрать несколько трендовых моделей: линейную, полином, нелинейную. Используя пошаговые процедуры отбора переменных, выбрана наиболее адекватная из них. В данном случае это линейная модель (нелинейная модель и полином, приведены в Приложении 3).

Линейная модель имеет вид:

У=11,8+ 0,193*Т

Исследуя данную модель на адекватность при помощи коэффициента детерминации, критерия Фишера, критерия Стьюдента и проведения анализа остатков (см. Приложение 4), можно прийти к выводу, что поскольку общий и скорректированный коэффициенты детерминации достаточно близки к 1, то можно сделать вывод о достаточно сильном влиянии факторных признаков на результирующий показатель Y. Уравнение значимо по критерию Фишера. Рассмотрев критерий Стьюдента для коэффициентов регрессии β0 и β1 можно сделать вывод, что оба коэффициента также значимы. Выполняются 2 условия Гаусса-Маркова из 3. Таким образом, видно, что линейная модель достаточно адекватна, но, тем не менее, нельзя сказать, что она описывает поведение цен на бензин полностью. Поэтому обоснованным будет построение регрессии, выявляющую зависимость не только от времени, но и от других факторов.

При прогнозировании цен на бензин АИ-92 на следующие 4 периода, т.е. на апрель, май, июнь, июль 2007 года при помощи трендовой модели получены следующий данные:

Точечные прогнозы составляют 19,50655 руб. за литр в апреле, 19, 69912 руб. за литр в мае, 19, 8917 руб. за литр в июне и 20,08427 руб. за литр в июле. Соответствующие интервальные прогнозные значения представлены следующими интервалами [19,07;19,94], [19,25;20,15], [19,43;20,36] и [19,60; 20,57].

2.3. Построение регрессионных моделей. Прогнозирование при помощи регрессионных моделей.

Прежде чем проводить корреляционный анализ необходимо устранить долгосрочную тенденцию (тренд) в уровнях временных рядов. Для этого используется процедура взятия последовательных разностей, а дальнейший корреляционный анализ ведется с помощью остатков. Ряды проверяются на долгосрочную тенденцию с помощью коррелограммы. Изначальные и измененные коррелограммы представлены в Приложении 5. Были устранены долгосрочные тенденции во всех показателях. Только после этого был проведен корреляционный анализ.

По графикам функций (см. Приложение 6) можно сказать, что признаки Х1 (цены на нефть) и Х4 (ИПЦ) оказывают достаточно сильное прямое влияния на Y (цена на аи-92) в текущем периоде, а признак Х3 (объем производства нефти) оказывает значительное обратное влияние на Y с запаздыванием в 8 месяцев. Х2 (курс доллара США) оказывает незначительное влияние на зависимую переменную в периоде T-2, то есть с запаздыванием в 2 месяца. Таким образом, будет строиться зависимость Y от Х1, Х2t-2, Х4 и Х3t-7.

ЛИНЕЙНАЯ МОДЕЛЬ

 Скачать реферат