Математические методы в экономике
3.4. Свободные коэффициенты bi (i =1, . ,m) уравнений ограничений (столбец B). В этом же столбце находим оптимальный план задачи.
3.5. Элементы a ij (i = 1, . ,m ; j = 1, . ,n) матрицы условий задачи (столбцы A1, , An ).
Таблица 1
|
Аб |
Сб < /td> |
В |
c1 |
. |
cj |
. |
ck |
. |
cn |
|
A1 |
. |
Aj |
. |
Ak |
. |
An | |||
|
А1 |
c1 |
b1 |
a11 |
. |
a1j |
. |
a1k |
. |
a1n |
|
… |
. |
. |
. |
. |
. |
. |
. |
. |
. |
|
Аi |
ci |
bi |
ai1 |
. |
aij |
. |
aik |
. |
ain |
|
… |
. |
. |
. |
. |
. |
. |
. |
. |
. |
|
Ar |
cr |
br |
ar1 |
. |
arj |
. |
ark |
. |
arn |
|
… |
. |
. |
. |
. |
. |
. |
. |
. |
. |
|
Am |
cm |
bm |
am1 |
. |
amj |
. |
amk |
. |
amn |
|
m+1 |
S |
S1 |
. |
Sj |
. |
Sk |
. |
Sn |
3.6. Оценки Sj (j=1, . ,n) векторов условий Aj , которые определяются по формуле:
где ci - весовые коэффициенты при базисных переменных.
Из этой формулы следует, что коэффициенты zj вычисляются для каждого столбца как сумма почленных произведений коэффициентов ci на одноименные коэффициенты j-го столбца. При заполнении симплекс-таблицы при условии, что рассматривается задача максимизации целевой функции, необходимо иметь в виду:
• если Sj ³ 0 для всех j = 1, ., n, то полученное решение является оптимальным;
• если имеются Sj < 0 и в столбцах Aj, соответствующих этим отрицательным оценкам, существует хотя бы один элемент aij > 0, то возможен переход к новому решению, связанному с большим значением целевой функции;
• Из отрицательных оценок выбирают ту, у которой значение по абсолютной величине больше. Если имеется несколько одинаковых отрицательных оценок, то выбирают ту, которой соответствует максимальный коэффициент целевой функции ci.
• если имеются Sk<0 и в столбце Ak все элементы aik £ 0, то в области допустимых решений целевая функция не ограничена сверху.
4. Определяется вектор Ak, который необходимо ввести в базис для улучшения решения, по наибольшему значению Sk . Переменная этого столбца xk будет новой базисной переменной, которая вводится в базис. Столбец, содержащий эту переменную, называетсянаправляющим столбцом.
5. Определяется вектор, который нужно вывести из базиса, используя равенство:
Это условие позволяет найти направляющую строку. Переменная xr, соответствующая этой строке, выводится из базисного решения и заменяется переменной xk направляющего столбца. Элемент ark, который стоит на пересечении направляющего столбца и направляющей строки, называется разрешающим элементом.
6. Заполняется таблица соответствующая новому базисному решению. В этой таблице, прежде всего заполняются клетки строки r с вводимой переменной xk. Для этого все элементы этой строки делятся на направляющий элемент. Получаются элементы новой строки:
br/ark, ar1/ark , . , arn/ark.
Остальные элементы новой таблицы определяются по правилу прямоугольника:
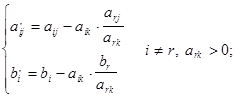 |
Другие рефераты на тему «Экономико-математическое моделирование»:
Поиск рефератов
Последние рефераты раздела
- Выборочные исследования в эконометрике
- Временные характеристики и функция времени. Графическое представление частотных характеристик
- Автоматизированный априорный анализ статистической совокупности в среде MS Excel
- Биматричные игры. Поиск равновесных ситуаций
- Анализ рядов распределения
- Анализ состояния финансовых рынков на основе методов нелинейной динамики
- Безработица - основные определения и измерение. Потоки, запасы, утечки, инъекции в модели
