Математические методы в экономике

Критерий оптимальности решения для нахождения максимального значения целевой функции: если в выражении линейной функции через неосновные переменные отсутствуют положительные коэффициенты при неосновных переменных, то решение оптимально.

Критерий оптимальности решения для нахождения минимального значения целевой функции: если в выражении линейной функции через неосновные переменные отсутству

ют отрицательные коэффициенты при неосновных переменных, то решение оптимально.

§3. «Метод искусственного базиса».

Если ограничения исходной задачи содержат единичную матрицу порядка М, то при неотрицательности правых частей уравнений определен первоначальный план, из которого с помощью симплекс – таблиц находится оптимальный план.

Если ограничения можно привести к виду:

Ах≤А0 при А0≥0, то система ограничений содержит единичную матрицу всегда.

Если задача не содержит единичной матрицы и не приводится к указанному виду, то для решения задачи используется метод искусственного базиса.

Для получения единичной матрицы к каждому ограничению прибавляют по одной неотрицательной переменной, которые называются искусственными. Единичные вектора, соответствующие искусственным переменным, образуют искусственный базис.

В целевую функцию искусственные переменные добавляются с коэффициентом М, если задана задача на нахождение минимума. В этом случае величина М предполагается достаточно большим положительным числом. Если необходимо найти минимальное значение целевой функции, то искусственные переменные записывают с коэффициентом (-М), который предполагается достаточно малым отрицательным числом. Для нахождения оптимального плана в случае, если заранее не задана величина М, применяется симплекс-метод, который в таблице имеет на одну строку больше, чем обычная симплекс-таблица.

Строка оценок разбивается на две:

(m+1) – оценка, не зависящая от М;

(m+2) – коэффициент при М.

По (m+2) строке определяют вектор, подлежащий включению в базис. Итерационный процесс проводят до исключения из базиса всех искусственных векторов. Затем процесс продолжают по (m+1) строке обычным симплекс-методом.

§4. «Транспортная задача»

Классическая транспортная задача формулируется следующим образом:

Имеется m пунктов отправления (производства) A1, A2, . ,Am, в которых расположены запасы некоторого однородного продукта (груза). Объём этого продукта в пункте Ai составляет ai единиц. Кроме того, имеется n пунктов потребления B1, B2, . ,Bn. Объём потребления в пункте Bj составляет bj единиц. Предполагается, что из каждого пункта отправления возможна транспортировка продукта в любой пункт потребления. Известна также стоимость cij перевозки единицы продукта из пункта Ai в пункт Bj .

Требуется составить такой план перевозок, при котором все заявки пунктов потребления полностью выполнялись бы пунктами отправления, а общая стоимость перевозок была минимальной.

При такой постановке данную задачу называют транспортной задачей по критерию стоимости.

В общем виде исходные данные представлены в таблице 9.

Таблица 9

Транспортная задача называется закрытой, если суммарный объем отправляемых грузов равен суммарному объему потребности в этих грузах по пунктам назначения

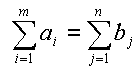
Если такого равенства нет (потребности выше запасов или наоборот), задачу называют открытой.

П.1 Алгоритм метода минимального элемента.

1. Из распределительной таблицы 9 выбирают наименьшую стоимость и в клетку, которая ей соответствует, помещают меньшее из чисел ai или bj (если таких клеток несколько, то выбирают любую);

2. Из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и то и другое;

3. Из оставшейся части таблицы снова выбирают наименьшую стоимость и процесс продолжается до тех пор, пока все запасы не будут вывезены, а потребности удовлетворены;

4. Рассчитывают транспортные расходы: сумма произведений количества перевезенной продукции на стоимость для занятых клеток.

П. 2 Алгоритм метода Фогеля.

1. В каждой строке находят разность между двумя наименьшими стоимостями и записывают ее около соответствующей строки справа;

2. В каждом столбце находят разность между двумя наименьшими стоимостями и записывают ее под соответствующим столбцом;

3. Среди всех полученных разностей находят максимальную и распределяют объем перевозки в клетку строки или столбца с наименьшей стоимостью;

4. Исключают из рассмотрения строку или столбец с распределенными поставками и возвращаются к пункту 1. Процесс продолжается до тех пор, пока все запасы не будут вывезены, а потребности удовлетворены;

5. Когда план построен, рассчитываются транспортные расходы.

П.3 Алгоритм метода двойного предпочтения.

1. В таблице 9 в каждом столбце отмечают галочкой клетку с наименьшей стоимостью и в каждой строке отмечают галочкой клетку с наименьшей стоимостью;

2. В клетки с двумя галочками записывают максимально возможные объемы перевозок, каждый раз, исключая соответствующий столбец или строку;

3. Распределяют перевозки по клеткам с одной галочкой;

4. В оставшейся части таблицы перевозки распределяют в клетки с наименьшей стоимостью.

5. Когда план построен, рассчитываются транспортные расходы.

П.4. Алгоритм метода северо-западного угла.

1. Пользуясь таблицей 9 распределяют груз, начиная с левой верхней, условно называемой северо-западной, клетки (1,1). Необходимо удовлетворить потребности В1 за счет поставщика А1;

2. а). Если b1>a1, в клетку (1,1) записывают a1 и строку 1 вычеркивают из рассмотрения;

b). Если a1>b1, в клетку (1,1) записывают b1 и столбец 1 вычеркивают из рассмотрения;

3. а). Если b1>a1, ∆= b1 - a1 – неудовлетворенные потребности. Спускаются на клетку вниз и сравнивают ∆ с a2;

b). Если a1>b1, ∆=a1 - b1 – не вывезенные запасы. Двигаются по строке вправо и сравнивают ∆ с b2;

4. Необходимо вернуться к пункту 2;

5. Рассчитываются транспортные расходы.

П.5. Алгоритм метода потенциалов.

1. проверяется тип модели транспортной задачи и в случае открытой модели сводим ее к закрытой;

2. находится опорный план перевозок путем составления 1-й таблицы одним из способов - северо-западного угла или наименьшей стоимости;

3. проверяем план (таблицу) на удовлетворение системе уравнений и на невыражденность; в случае вырождения плана добавляем условно заполненные клетки с помощью « 0 »;

4. для опорного плана определяются потенциалы ui и vj, соответствующие базисным клеткам, по условию:

ui + vj = cij

Таких уравнений будет m + n - 1 , а переменных будет m + n. Для их определения одну из переменных полагают равной любому постоянному значению. Обычно принимают u1 = 0.

 Скачать реферат