Исследование зависимости между объемом производства, капитальными вложениями и выполнением норм выработки

Точкой min Z будет точка первого касания линии уровня с допустимым многоугольником. Точкой max – точка отрыва линии уровня от допустимого многоугольника. Эти точки чаще всего совпадают с некоторыми вершинами допустимого многоугольника, хотя их может быть и бесчисленное множество, если линия уровня Z параллельна одной из сторон допустимого многоугольника. Это точка С (1,04; 3,28) Z=32,68 у.д.е.

Решим задачу с помощью симплекс-таблиц.

Пусть необходимо найти оптимальный план производства двух видов продукции P и R.

1. Построим оптимизационную модель:

F(X)=3X1+9X2→max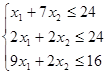

2. Преобразуем задачу в приведенную каноническую форму. Для этого введем дополнительные переменные X3, X4 и X5.

F(X)=3X1+9X2→max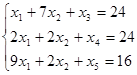

Построим исходную симплекс-таблицу и найдем начальное базисное решение.

Базисное решение (0; 0; 24;24; 16). F=0.

Находим генеральный столбец и генеральную строку

. Генеральный элемент 7

Базисное решение (0; 8; 4; 0; 10). F=40.

2,22222. Генеральный элемент 1,8.

Базисное решение (2,22; 7,56; 0; 0; 2,74). F=46,65.

Эта таблица является последней, по ней читаем ответ задачи. Оптимальным будет решение (2,22; 7,56; 0; 0; 2,74), при котором Fmax =46,65, т.е. для получения наибольшей прибыли, равной 46,65 денежных единиц, предприятие должно выпустить 2,22 единиц продукции вида P и 7,56 единиц продукции вида R, при этом ресурсы A и B будут использованы полностью, а 2,74 единиц ресурса С останутся неизрасходованными.

ЧАСТЬ 2

Постановка задачи

Исследовать зависимость между объемом производства, капитальными вложениями и выполнением норм выработки. Для построения модели собраны данные по исследуемым переменным на 12-ти предприятиях объединения.

Предполагая, что зависимость между переменными имеет линейный характер, анализ провести в следующей последовательности:

а) построить уравнение регрессии ;

б) построить уравнение регрессии ;

в) исследовать модели , и сделать соответствующие выводы;

 Скачать реферат