Решение заданий по высшей математике

Функция у = ¦(х)-непереодическая, если сущ такое число Т не равное нулю, что ¦(х+Т)=¦(х), при этом наименьшее положительное число Т наз-ся периодом

38. Бесконечно малые и бесконечно большие функции. Их свойства

Функция f(x) называется бесконечно малой при х®а, где а может быть числом или одной из величин ¥, +¥ или -¥, если .Бесконечно малой функция может быть только если указать к какому числу стремится аргумент х. При различных значениях а функция может быть бесконечно малой или нет.

Теорема. Для того, чтобы функция f(x) при х®а имела предел, равный А, необходимо и достаточно, чтобы вблизи точки х = а выполнялось условие f(x) = A + a(x),

где a(х) – бесконечно малая при х ® а (a(х)®0 при х ® а).

Свойства бесконечно малых функций:

1.Сумма фиксированного числа бесконечно малых функций при х®а тоже бесконечно малая функция при х®а.

2.Произведение фиксированного числа бесконечно малых функций при х®а тоже бесконечно малая функция при х®а.

3.Произведение бесконечно малой функции на функцию, ограниченную вблизи точки х = а является бесконечно малой функцией при х®а.

4.Частное от деления бесконечно малой функции на функцию, предел которой не равен нулю есть величина бесконечно малая.

Бесконечно большие функции

Предел функции f(x) при х®а, где а- число, равен бесконечности, если для любого числа М>0 существует такое число D>0, что неравенствоïf(x)ï>M

выполняется при всех х, удовлетворяющих условию0 < ïx - aï < D

Записывается .

Собственно, если в приведенном выше определении заменить условие ïf(x)ï>M на f(x)>M, то получим:а если заменить на f(x)<M, то:

Функция называется бесконечно большойпри х®а, где а – чосли или одна из величин ¥, +¥ или -¥, если , где А – число или одна из величин ¥, +¥ или -¥.

Связь бесконечно больших и бесконечно малых функций осуществляется в соответствии со следующей теоремой.

Теорема. Если f(x)®0 при х®а (если х®¥ ) и не обращается в ноль, то

35.Предел функции на бесконечности

Пусть функция f(x) определена на (a, + ∞). Число A называется пределом функции f(x) при x → + ∞ (обозначается A =

lim

x → + ∞

f(x) ), если  ε > 0  N:  x > N  |f(x) − a| < ε.

Пусть функция f(x) определена на ( − ∞,a).

Число A называется пределом функции f(x) при x → − ∞ (обозначается A =

lim

x → − ∞

f(x) }, если  ε > 0  N:  x < − N  |f(x) − a| < ε.

Если существуют пределы функции f(x) при x → + ∞ и при x → − ∞ и они равны одному и тому же числу A, то это число A называется пределом функции f(x) при x → ∞ {обозначается

A =

lim

x → ∞

f(x) .

Теоремы о пределах последовательностей и правила их вычисления распространяются и на пределы функций в бесконечности.

36. Предел функции в точке

Пусть функция f(x) определена в некоторой проколотой окрестности точки x0 .

Число A называется пределом функции f(x) при x → x0 (или в точке x0), если для любого ε > 0 найдется δ > 0 такое, что для всех x, для которых 0 < |x − x0| < δ, справедливо неравенство

|f(x) − A| < ε, т.е.

lim

x → x0

f(x) = A  ε > 0  δ > 0 : 0 < |x − x0| < δ |f(x) − A| < ε.

Используем понятие окрестности и учтем, что

0 < |x − x0| < δ x

•

O

δ (x0 ) и |f(x) − A| < ε f(x) Oε (A).

(Точка над символом окрестности указывает, что это проколотая окрестность.)

Теперь определение предела функции в точке можно представить в виде

lim

x → x0

f(x) = A  ε > 0  δ > 0 : x

•

Oδ (x0 )  f(x)  Oε (A).

10. Геометрическое представление комплексных чисел.

Действительные числа изображаются точками на числовой прямой:

Здесь точка A означает число –3, точка B – число 2, и O – ноль. В отличие от этого комплексные числа изображаются точками на координатной плоскости. Выберем для этого прямоугольные (декартовы) координаты с одинаковыми масштабами на обеих осях. Тогда комплексное число a+ bi будет представлено точкой Р с абсциссой а и ординатой b (см. рис.). Эта система координат называется комплексной плоскостью.

Модулем комплексного числа называется длина вектора OP, изображающего комплексное число на координатной (комплексной) плоскости. Модуль комплексного числа a+ bi обозначается | a+ bi | или буквой r и равен:

Сопряжённые комплексные числа имеют одинаковый модуль.

Аргумент комплексного числа - это угол между осью OX и вектором OP, изображающим это комплексное число. Отсюда, tan = b / a .

Тригонометрическая форма комплексного числа. Абсциссу a и ординату b комплексного числа a + bi можно выразить через его модуль r и аргумент :

Операции с комплексными числами, представленными в тригонометрической форме.

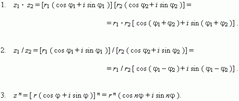
Это знаменитая формула Муавра.

Здесь k - целое. Чтобы получить n различных значений корня n-ой степени из z необходимо задать n последовательных значений для k ( например, k = 0, 1, 2,…, n – 1 ) .

8. Геометрический смысл действий над комплексными числами

Действия над комплексными числами имеют простой геометрический смысл. Начнём со сложения. Пусть число изображается точкой , - точкой , а - точкой (рис 3). Тогда , , . Таким образом, точка имеет координаты и, значит, .

 Скачать реферат