Основы дискретной математики

3.2.3 Вариантв заданий

c="images/referats/12447/image132.png">

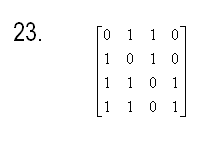
3.3 Вопросы для самопроверки

1) Какие операции над графами Вы знаете?

2) Как формируется матрица смежности?

3) Как формируется матрица весов?

4) Как формируется матрица достижимости?

5) Как формируется матрица инцидентности?

6) Перечислите основные понятия, относящиеся к графам-деревьям.

7) Приведите пример сортировки и поиска в деревьях.

8) Для чего применяется алгоритм, подобный алгоритму Дейкстры, в коммуникационных сетях?

9) Перечислите известные Вам алгоритмы обхода графов.

10) Что такое транспортная сеть? Приведите пример.

11) Какой граф называется эйлеровым? Приведите пример эйлерова графа.

12) Какой граф называется гамильтоновым? Приведите пример гамильтонова графа.

13) Какой вид отношений на графах представляет изоморфизм графов?

14) Приведите пример отношения порядка и отношения эквивалентности на графе.

15) Какие алгоритмы обхода графов Вам известны?

16) Какие виды графов Вы знаете?

17) Что понимается под степенью вершины?

18) Как определяются числа внутренней и внешней устойчивости графа?

19) Как определяются хроматическое и цикломатическое числа графа?

20) Сформулируйте транспортную задачу и связанные с ней понятия?

21) Опишите кратко алгоритм управления проектами.

22) Приведите пример построения разреза графа.

23) Приведите пример дерева с корнем.

Практическая работа № 4. Элементы теории множеств и алгебры логики

Цель работы: применение знаний теории множеств и алгебры логики для решения практической задачи.

4.1 Указание к выполнению

Данная практическая работа сочетает в себе использование элементов теории множеств и алгебры логики. Все теоретические сведения, необходимые для выполнения данной работы, изложены в лекциях и в уже изданных методических пособиях [23], [25]. Выполнение данной работы рекомендуется выполнять по образцу, рассмотренному далее.

4.2 Задание к работе

1. Составить множества из букв Ф.И.О

2. Представить полученные множества на кругах Эйлера.

3. Представить буквы Ф.И.О. в двоичной системе.

4. Представить диаграмму Венна. СНДФ.

5. Перевести числа даты рождения в двоичную систему счисления.

Примечание: желательно реализовать основные вычисления в приложении на Delphi.

4.3 Практическая часть

Пример 1:

1 Множества из букв Ф.И.О.

МОРОЗОВ ОЛЕГ ЕВГЕНЬЕВИЧ

Ф = {М, О, Р, З, В};

И = {О, Л, Е, Г};

О = {Е, В, Г, Н, Ь, И, Ч};

2 Круги Эйлера и диаграммы Венна

Рисунок 4.1 – Круги Эйлера

Таблица 4.1 – Буквы алфавита в двоичной системе

 Скачать реферат