Расчет гидравлической циркуляционной установки

4.1.1 Определение расхода жидкости

Расходом потока называется количество жидкости, протекающее через некоторое поперечное сечение потока в единицу времени. Это сечение должно быть сделано так, чтобы обязательно пересекало каждую элементарную струйку и только один раз. Обычно за поверхность сечение принимают живое сечение потока. Для аналитического вычисления расхода необходимо знать

закон распределения скоростей по сечению потока.

Наиболее простыми и вместе с тем точными способами измерения расхода жидкости являются объемный и весовой способы.

При весовом способе взвешиванием на весах находят вес всей жидкости, поступившей в мерник за определенное время, определяют весовой расход по формуле, и, зная удельный вес жидкости, вычисляют объемный расход.

В практике, как правило, для измерения расхода жидкости пользуются специальными приборами, которые предварительно тарируются объемным или весовым способом.

Одним из таких основных приборов является трубчатый водомер, или водомер Вентури. Большим достоинством этого водомера является простота конструкции и отсутствие в нем каких-либо движущихся частей. Трубчатые водомеры могут быть горизонтальными и вертикальными.

Для определения расхода жидкости рассмотрим ртутный дифманометр расходомера Вентури.

Запишем уравнение неразрывности для сечений 1-1 и 2-2:

Q1 = Q2, следовательно 1 · S1 = 2 ·S2 (5)

Из полученного равенства выразим скорость V2:

2 = 1· S1/S2 (6)

Запишем уравнение Бернулли для двух сечений 1-1 и 2-2:

(7)

где z1 и z2 - расстояния от сечений А-А - и В-В соответственно до некоторой произвольно выбранной горизонтальной плоскости; р-давления в сечениях А-А и В-В соответственно; ρ-плотность циркулирующей жидкости; g-ускорение свободного падения; - скорость течения жидкости в сечениях А-А и В-В соответственно; α-силы Кориолиса, которые учитывают неравномерность распределения скоростей в сечениях А-А и В-В соответственно; hА-В - потери напора на участках между выбранными сечениями. Выберем ось трубопровода за начало отсчета, тогда z1=z2=0, т.к трубопровод горизонтален. Предположим, что по трубопроводу течет идеальная жидкость. Тогда потери напора hА-В = 0.

α1 = α2 = 1.

Теоретический расход будет меньше, т.к существуют потери напора. Учтем это с помощью поправочного коэффициента, который называется коэффициентом расхода μ.

(8)

С учетом всех преобразований:

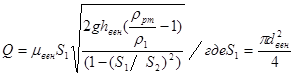(9)

В итоге имеем:

(10)

Q= 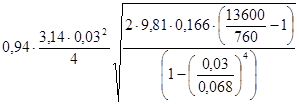=0,005 м³/с

4.1.2 Определение потерь напора

Определение величины потерь напора при движении реальных жидкостей является одной из основных задач практической гидравлики. При движении реальной жидкости энергия движения (напор) жидкости будет убывать по направлению движения. Причиной этого являются затраты энергии на преодоление сопротивлений движению, обусловленные внутренним трением в вязкой жидкости. В гидравлике различают два основных вида сопротивлений:

1. Потери напора по длине, т.е. сопротивления, проявляющиеся по всей длине потока, обусловленные силами трения частиц жидкости друг о друга и о стенки, ограничивающие поток. Это линейные потери. Они определяются по формуле Дарси-Вейсбаха:

(11)

где - длина трубы (или участка трубы) на котором определяются потери напора"; - диаметр трубы; - средняя скорость в трубе; λ = λ (Re, ∆/d) - коэффициент гидравлического сопротивления трения. Коэффициент гидравлического сопротивления трения (λ) зависит от двух безразмерных параметров Rе - числа Рейнольдса и ∆/d - относительной шероховатости трубы. Число Рейнольдса определяется по формуле:

(12)

где μ - динамическая вязкость жидкости (Па·с); - кинематическая вязкость жидкости (м²/с). Для определения коэффициента гидравлического сопротивления трения существуют много различных формул. Удобно пользоваться следующими формулами. Для ламинарного режима движения:

λ =64/Rе, Rе < 2000÷2320.

Для турбулентного режима движения (формула Альтшуля):

λ=0,11 (68/Rе+ ∆/d) , Rе >2000÷2320

2. Местные потери напора, так называемые местные сопротивления, обусловленные различного рода препятствиями, устанавливаемыми в потоке (задвижка, кран, колено), приводящими к изменениям в величине или направлении скорости течения жидкости. Потери напора на местных сопротивлениях определяются по формуле

(м) (13)

где - средняя скорость движения жидкости;

- коэффициент местного сопротивления.

Потеря напора на местном сопротивлении может определяться как по скорости до местного сопротивления, так и по скорости после местного сопротивления. Так как скорости по величине могут быть разными, то в этих случаях для одного и того же местного сопротивления будут разные значения . Принято определять потери напора по скорости после местного сопротивления. Исключение составляет расширение трубопровода (выход потока из трубы в бак), где потери определяются по скорости до местного сопротивления.

Для определения потерь напора по данной курсовой работе будем учитывать как потери напора по длине трубопровода, так и местные сопротивления.

 Скачать реферат