Расчет гидравлической циркуляционной установки

На всасывающей линии насосной установки имеется всасывающая коробка с обратным клапаном 1, поворотное колено 2, задвижка 3, вакуумметр Рв. На нагнетательной линии установлены манометры Рм1, Рм2, Рм3, скоростная трубка 5 и расходомер Вентури 6. Промежуточная емкость С в донной части имеет насадок 7.

ИСХОДНЫЕ ДАННЫЕ

3. Схема установки

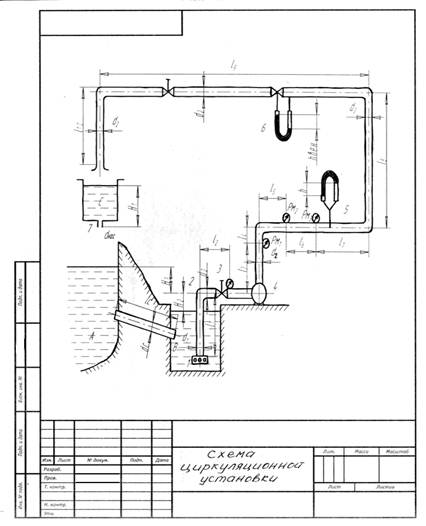
4. Расчет циркуляционной установки

4.1 Определение геометрической высоты всасывания насоса Н2

Для определения геометрической высоты воспользуемся известным уравнением Бернулли. Для его применения необходимо выбрать плоскость сравнения. Плоскостью сравнения может служить любая горизонтальная плоскость. Также необходимо выбрать два сечения. Сечения проводятся перпендикулярно вектору скорости. Нумерация сечений производится по направлению движения жидкости. Уравнение Бернулли для установившегося движения реальной несжимаемой жидкости записывается:

(1)

где: z-расстояние от выбранных сечений соответственно до некоторой произвольно выбранной плоскости сравнения (м). Если сечение лежит ниже плоскости сравнения, то z отрицательна.

р - абсолютное или манометрическое давление в сечениях (Па);

ρ - плотность несжимаемой жидкости (кг/м³);

α - коэффициент кинетической энергии (коэффициент Кориолиса). Обычно принимается равным единице.

- средняя скорость в сечениях (м/с);

g - ускорение свободного падения (м/с²);

h1-2 - потери напора между сечениями. Они представляют собой сумму потерь напора по длине и сумму потерь напора на местных сопротивлениях:

h1-2 = hм + hд

На схеме циркуляционной установки удобно выбрать два сечения, где:

А-А это поверхность жидкости в нижнем резервуаре В;

В-В в месте установки вакуумметра Рв во всасывающей линии насосной установки.

Тогда уравнение Бернулли для этих сечений запишется в виде:

(2)

где zА-А и zВ-В - расстояния от сечений А-А и В-В соответственно до некоторой произвольно выбранной горизонтальной плоскости;

РА-А, РВ-В - давления в сечениях А-А и В-В соответственно;

ρ - плотность циркуляционной жидкости;

g - ускорение свободного падения;

А-А и В-В - скорость течения жидкости в сечении А-А и В-В соответственно;

hА-В - потери напора на участках между выбранными сечениями.

Если выбрать поверхность жидкости в нижнем резервуаре за начало отсчета, т.е. сечение А-А, тогда zА-А=О, а zВ-В=Н2.

Поскольку в нижнем резервуаре (В) уровень установившийся, значение скорости будет равным нулю. А так как резервуар открыт, то давление в сечении А-А можно принять равным атмосферному РА-А=Ратм. Давление же в сечении В-В представляет собой разность атмосферного и вакуумного давления РВ-В =Ратм - Рвак. При решении практических задач коэффициент Кориолиса (α), как уже говорилось, можно принять равным единице и в расчетах не учитывать. Тогда в уравнении Бернулли остается лишь одна неизвестная величина - скорость в. Скорость определяется по формуле

(3)

где Q - расход жидкости (м³/с);

S - площадь поперечного сечения (м²);

В результате, формула (2) примет вид:

(4)

В полученной формуле известны все величины, кроме Н2 и hА-В. Поэтому для определения геометрической высоты всасывания насоса (Н2) предварительно необходимо определить hА-В.

 Скачать реферат