Статистика процесса использования товаров населением

(20)

(21)

(22)

(23)

(24)

ight=44 src="images/referats/14048/image070.png">(25)

(26)

(27)

Коэффициент линейной корреляции, равный 0,997, свидетельствует о наличии очень сильной связи.

3.2. Оценка существенности коэффициента корреляции. Для этого найдем расчетное значение t-критерия Стьюдента:

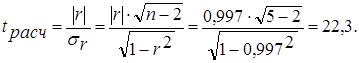(28)

По таблице критических точек распределения Стьюдента найдем tкр при уровне значимости α=0,05 и числе степеней свободы ν = 5-k-1 = 5-1-1=3. tкр = 3,18. Так как tрасч > tкр (22,3> 3,18), то линейный коэффициент считается значимым, а связь между x и y – существенной.

4. Построение уравнения регрессии.

Этап построения регрессионного уравнения состоит в идентификации (оценке) его параметров, оценке их значимости и значимости уравнения в целом.

4.1. Идентификация регрессии. Построим линейную однофакторную регрессионную модель вида Для оценки неизвестных параметров a0, a1 используется метод наименьших квадратов, заключающийся в минимизации суммы квадратов отклонений теоретических значений зависимой переменной от наблюдаемых (эмпирических).

Система нормальных уравнений для нахождения параметров a0, a1 имеет вид:

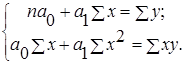(29)

После преобразования системы получим:

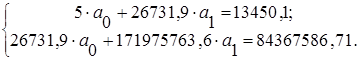(30)

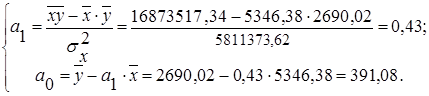(31)

Решением системы являются значения параметров: а0 = 391,08; a1 = 0,43.

Уравнение регрессии:

(32)

Коэффициент детерминации:

Таким образом, судя по регрессионному коэффициенту а1=0,43, можно утверждать, что с увеличением дохода на 1 рубль потребительские расходы увеличивается в среднем на 0,43 рублей в месяц. Коэффициент регрессии а0=391,08 учитывает влияние факторов, неучтенных в модели. В нашем случае влияние неучтенных факторов невелико.

Коэффициент детерминации показывает, что 99,4% вариации признака «потребительские расходы» обусловлено вариацией признака «доход а остальные 0,6% вариации связаны с воздействием неучтенных факторов.

4.2. Проверка значимости параметров регрессии.

Для того, чтобы оценить на сколько параметры а1, а0 отображают исследуемый процесс и не являются ли эти значения результатом случайных величин, рассчитаем средние ошибки и t-критерии Стьюдента.

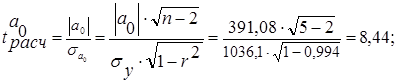(33)

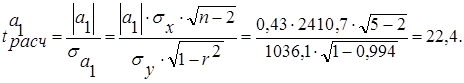(34)

По таблице критических точек распределения Стьюдента найдем tкр при уровне значимости α=0,05 и числе степеней свободы ν = 3. tкр = 3,18. Так как tа0расч > tкр (8,44 >3,18), то параметр а0 считается значимым. Так как tа1расч > tкр (22,4 > 3,18), то параметр а1 считается значимым.

4.3. Проверка значимости уравнения регрессии в целом.

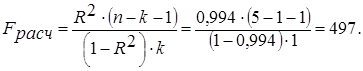(35)

По таблице критических значений критерия Фишера найдем Fкр = 10,13 (при α=0,05, ν1=k=1, ν2=n-k-1=3). Так как Fрасч > Fкр (497 > 10,13), то для уровня значимости α=0,05 и числе степеней свободы ν1=1, ν2=7 построенное уравнение регрессии можно считать значимым.

5. Использование регрессионной модели для принятия управленческих решений (анализа, прогнозирования и т.д.).

Вычислим прогнозное значение потребительских расходов для величины дохода хр=10000. При уровне значимости α=0,05 точечное значение прогноза

(36)

Т.е. с доверительной вероятностью p=1-α=1-0,05=0,95 можно предполагать, что прогнозное значение потребительских расходов при величине дохода, равной 10000 рублей, составит около 4691,08 рублей.

Таким образом, в результате проведения корреляционно-регрессионного анализа показано, что между величиной дохода и величиной потребительских расходов существует тесная связь. Изучаемые признаки связаны линейной корреляционной зависимостью. Найдены параметры этой зависимости. Проведена комплексная оценка значимости, как параметров регрессионного уравнения, так и регрессии в целом. Показана адекватность построенного уравнения регрессии. Следовательно, регрессионная модель зависимости величины дохода и величины потребительских расходов может быть использована для принятия управленческих решений.

2.5 Методы выявления тренда

Тренд – основная тенденция развития социально – экономического явления. К методам, позволяющим выявить тренд относятся:

1. метод укрупнения интервалов;

2. метод скользящей средней;

3. метод аналитического выравнивания и некоторые другие.

Рассмотрим перечисленные выше методы. Исходные данные приведены в таблице 9.

Таблица 9 Потребительские расходы по месяцам

 Скачать реферат