Построение регрессионной модели

Найдем дисперсию переменных:

= 9448,5 – 88,332 = 1646,31

= 27,506 – 5,2352 = 0,0955

Найдем параметров А и В регрессии составили:

b =0,00314

5,325 – 0,00314 · 88,33 = 4,958

Получено линейное уравнение:

= 4,958 + 0,00314 · х

Произведем потенцирование полученного уравнения и запишем его в обычной форме:

= e4,958 · e0,00314 · х = 142,31 · e0,00314 х

Тесноту связи оценим через индекс корреляции рху:

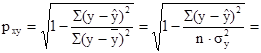
0,436

Связь средняя.

Определим коэффициент детерминации:

0,1838

Т.е. вариация результативного признака на 18,38% объясняется вариацией факторного признака.

Найдем среднюю ошибку аппроксимации:

25,9%

Средняя ошибка аппроксимации имеет значение меньше 30%, т.е. надежность уравнения средняя.

Рассчитаем F-критерий: (m – число параметров при переменной x)

1,8378

Fкр = 4,964

Т.к. Fкр > Fфакт, т.е. необходимо отклонить гипотезу о статистической значимости параметров уравнения.

Найдем стандартную ошибку остаточной компоненты по формуле:

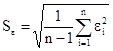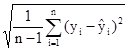= = = 55,77

Найдем средние квадратичные (стандартные) ошибки оценивания коэффициента b и свободного члена а уравнения регрессии:

40,45

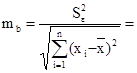
0,416

Найдем t – критерий Стьюдента для обоих параметров:

142,31 / 40,45 = 3,518

0,00314 / 0,411 = 0,0076

Сравнивая значения t-статистики для каждого из коэффициентов линейной регрессии с табличным значением (α = 0,05; k = 12) tтабл = 2,228, можно сказать, что с вероятностью 95% коэффициент а надёжен, коэффициент b ненадёжен при данном уровне значимости.

Для расчета доверительного интервала определяем предельную ошибку Δ:

= tтабл · = 2,228 * 40,45 » 90,12

= tтабл · = 2,228 * 0,0076 » 0,0169

Доверительные интервалы для коэффициентов регрессии:

a – Δa < a < a + Δa

52,19 < a < 232,43

b – Δb < b < b + Δb

– 0,01376 < b < 0,02004

Построим линию показательной зависимости на поле корреляции:

Рис. 2. Рассчитанные линии регрессий

У линейной зависимости меньше стандартная ошибка и больше значение F-критерия. Поэтому из двух уравнений регрессий линейное более достоверно. Но низкая надежность коэффициента регрессии b, говорит, что результаты аппроксимации будут иметь достаточно низкую надежность (80%).

 Скачать реферат