Построение регрессионной модели

Найдем дисперсию переменных:

= 9448,5 – 88,332 = 1646,31 (тыс. руб.)2

= 42261,83 – 196,832 = 3519,78 (тыс. руб.)2

Найдем параметры a и b уравнения линейной регрессии:

ight=44 src="images/referats/14070/image013.png">0,667

196,83 – 0,667 · 88,33 = 137,91 тыс. руб.

Уравнение регрессии:

= 137,91 + 0,667 · х

Построим линию регрессии на рис. 1.

С увеличением прожиточного минимума на 1 тыс. руб. пенсия увеличивается на 0,667 тыс. руб.

Рассчитаем линейный коэффициент парной корреляции:

0,456

Т.к. коэффициент в интервале от 0,3 до 0,7 связь средняя, прямая.

Определим коэффициент детерминации:

(0,456)2 = 0,208

Т.е. вариация пенсий на 20,8% объясняется вариацией прожиточного минимума.

Найдем среднюю ошибку аппроксимации:

26,7%

Средняя ошибка аппроксимации имеет значение меньше 30% – это говорит о среднем уровне надежности уравнения регрессии.

Рассчитаем F-критерий:

2,628

Критическое значение распределения Фишера определяют либо по таблицам распределения Фишера, либо расчетным путем с использованием функции FРАСПОБР() табличного процессора Excel. Для уровня доверия 0,95, одного фактора и 12 значений:

Fкр = F (0,05; 1; 10) = 4,964

Т.к. Fкр > Fфакт, то необходимо отклонить гипотезу о статистической значимости параметров уравнения. Т.е. использовать данную функцию для аппроксимации нельзя.

Найдем стандартную ошибку остаточной компоненты по формуле:

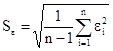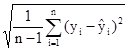= = = 55,14

Найдем средние квадратичные (стандартные) ошибки оценивания коэффициента b и свободного члена а уравнения регрессии:

39,99

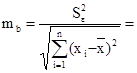
0,411

Найдем t – критерий Стьюдента для обоих параметров:

137,91 / 39,99 = 3,448

0,667 / 0,411 = 1,623

Сравнивая значения t-статистики для каждого из коэффициентов линейной регрессии с табличным значением (α = 0,05; k = 12) tтабл = 2,228, можно сказать, что с вероятностью 95% коэффициент а надёжен, коэффициент b ненадёжен при данном уровне значимости.

Для расчета доверительного интервала определяем предельную ошибку Δ:

= tтабл · = 2,228 * 39,99 » 89,1

= tтабл · = 2,228 * 0,411 » 0,916

Доверительные интервалы для коэффициентов регрессии:

a – Δa < a < a + Δa

48,81 < a < 227,01

b – Δb < b < b + Δb

– 0,249 < b < 1,583

Таким образом, полученные оценки коэффициента регрессии b не являются эффективными и состоятельными, а само уравнение = 137,91 + 0,667·х не может использоваться для моделирования и прогнозирования динамики.

Это обусловлено большой ошибкой уравнения регрессии.

Для построения уравнения показательной кривой у = а · еbх линеризуем переменные логарифмированием обеих частей уравнения:

ln у = ln а + b·x

Y = A + b·x

Где Y = ln y, A = ln a.

Для расчетов будем использовать данные таблицы 4.

Таблица 4

 Скачать реферат