Линейное программирование

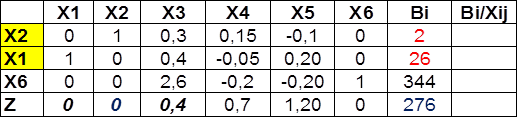
III опорное решение.

x1=26, x2=2, x3=0, x4=0, x5=0, x6=344, Z=276.

Третье опорное решение является оптимальным, так как последняя строка симплекс таблицы содержит только положительные элементы.

Подставляем в линейную функцию Z = 10*26 + 8*2 + 6*0 = 276.

Оптимально производить Товар 1 – в количестве 26, Товар

2 – в количестве 2 и Товар 3 – в количестве 0.

Запрограммируем в MS Office Excel (Приложение№1) и в Pascal (Приложение№2). Данные и условия сформированы ранее.

Заключение

Несмотря на то, что симплекс-метод является достаточно эффективным алгоритмом, показавшим хорошие результаты при решении прикладных задач ЛП, он является алгоритмом с экспоненциальной сложностью. Причина этого состоит в комбинаторном характере симплекс-метода, последовательно перебирающего вершины многогранника допустимых решений при поиске оптимального решения. Тем не менее, сам факт полиномиальной сложности задач привёл к созданию целого класса эффективных алгоритмов ЛП — методов внутренней точки, первым из которых был алгоритм Н. Кармаркара, предложенный в 1984 г. Метод внутренних точек, который, в отличие от симплекс-метода, обходит точки из внутренней части области допустимых значений, использует методы логарифмических барьерных функций нелинейного программирования, разработанные в 60-х гг. Фиако (Fiacco) и МакКормиком (McCormick). Первый полиномиальный алгоритм, метод эллипсоидов, был предложен в 1979 г. советским математиком Л. Хачияном, разрешив таким образом проблему, долгое время остававшуюся нерешённой. Метод эллипсоидов имеет совершенно другую, некомбинаторную, природу, нежели симплекс-метод. Однако в вычислительном плане этот метод оказался неперспективным.

Список использованной литературы

А.И.Ларионов, Т.И.Юрченко “Экономико-математические методы в планировании: Учебник – М.: Высш.школа, 1984

Томас Х. Кормен и др. Глава 29. Линейное программирование // Алгоритмы: построение и анализ = INTRODUCTION TO ALGORITHMS. — 2-е изд. — М.: «Вильямс», 2006.

В.И. Бодров, Т.Я. Лазарева, Ю.Ф. Мартемьянов «Математические методы принятия решений», Издательство ТГТУ, 2004

Вершик А. М. «O Л. В. Канторовиче и линейном программировании»

Большакова И. В., Кураленко М. В. «Линейное программирование. Учебно-методическое пособие к контрольной работе».

 Скачать реферат