Совершенствование системы управления охраной окружающей среды

Моделированию переноса загрязнений в городах посвящено множество работ отечественных и зарубежных специалистов. Наиболее распространена следующая методика построения полей загрязнений.

Для городской территории описываются характеристики основных источников выбросов – ТЭЦ, РТС, заводов, автотрасс и т. п. Описывается городской ландшафт, параметры застройки, метеорологическая ситуация. Использ

уя специальные формулы расчетов рассеивания примесей в атмосфере, вычисляют концентрации загрязняющих примесей в каждой точке и строятся поля загрязнений. Модели и программы расчета по данной методике называются обычно экстраполяционными.

Для оперативных расчетов полей загрязнений атмосферы можно использовать также следующую методику. В некоторых точках города с помощью стационарных автоматических станций измеряются концентрации загрязняющих примесей в воздухе. Затем с учетом городского ландшафта и метеообстановки рассчитываются значения концентраций примесей в точках, расположенных между каждыми двумя близлежащими станциями. На основании расчетных и реальных данных строятся поля загрязнений. Так как для расчета используются методы интерполяции, то модели и программы называются интерполяционными.

Большое практическое значение имеет и решение обратной задачи, при которой по данным предельным концентрациям определяется мощность источника, дающего такие значения. Обратная задача решается при расчете т. н. ПДВ – предельно допустимых выбросов предприятий, на основании которых в России устанавливаются размеры платежей в экологические фонды.

Рассмотрим математические аспекты, а также вопросы точности различных моделей.

В экстраполяционных моделях расчет рассеивания от точечных источников строится на базе т. н. уравнений баланса. Суть уравнения баланса можно иллюстрировать простым примером. Пусть внутри объема V, например, шара, с поверхностью S находится источник вещества с удельной концентрацией а и скоростью притока е. Обозначим скорость движения вещества по нормали к поверхности пространства (шара) через А, элемент объема – через dV, а элемент поверхности – dS. Тогда процесс рассеивания в пространстве описывается простым уравнением.

(2.2)

Объемный интеграл в левой части уравнения задает скорость изменения количества вещества в данном объеме (r - удельная плотность вещества). Первый интеграл в правой части есть полный поток вещества через поверхность S, а второй интеграл - приток вещества в объеме V.

С этим уравнением можно проводить преобразования с целью учета реальных условий города. Можно задавать разные скорости переноса по разным направлениям, имитируя ветер, можно вводить турбулентность, имитируя рельеф, можно вводить т. н. коэффициенты шероховатости подстилающей поверхности. Так как прямое вычисление интегралов весьма трудоемко, используются косвенные методы, такие как различные численные модели, стохастическое моделирование методом Монте-Карло и т. д.

Точность всех типов моделей определяется масштабом и точностью описания исходных и граничных условий. Масштаб модели - это та единица общей территории, относительно которой определяется концентрация. Если это десятки и сотни квадратных метров, то говорят о микромасштабе, если квадратные километры, то это мезомасштаб, а если десятки квадратных километров, то макромасштаб.

На моделях макромасштаба легче достигается высокая точность. Содержательно в этом случае как бы рассматривается ровная гладкая поверхность, и на большой высоте, такой, что можно пренебречь шероховатостью поверхности, находится единственный источник выбросов. Модель будет простой, и точность ее будет высокой. Если же рассматривается город и источник выбросов находится на небольшой высоте, то для достижения высокой точности необходимо учитывать турбулентность, возникающую в уличных каньонах, вокруг домов, складках естественного рельефа, т. е. модель будет усложняться.

Для того, чтобы в реальном времени с помощью эстраполирующих моделей в масштабах большого города проводить расчеты переносов загрязнений в атмосфере даже от стационарных источников, нужно знать текущие значения выбросов в атмосферу и направление ветров в микромасштабе. Для города, имеющего сотни источников выбросов, а в Москве сто одиннадцать тысяч источников выбросов, 12 ТЭЦ и 48 РТС, не считая средних и мелких предприятий и заводов, получение такой информации стоит дороже, чем установка в городе десятка стационарных автоматических станций контроля атмосферного воздуха. Это не означает, что эстраполяционные модели расчета не имеют практического значения. Они могут быть полезны при стратегическом планировании городской застройки, для расчета различных вариантов прокладки автотрасс, строительства новых городских объектов, но не для оперативных расчетов полей загрязнений.

К числу наиболее известных методов расчета распространения примесей в атмосфере относятся модели, основанные на гауссовском (нормальном) распределении случайных величин. В России к этому классу относится методика ОНД-86, признанная нормативным документом для расчета ПДВ. Многочисленные эксперименты показывают, что она может использоваться лишь для оценки максимально возможной наземной концентрации примесей при наихудших условиях рассеивания.

Для учета рельефа, вертикального профиля температуры, других метеоусловий разрабатываются более сложные модели, такие как гидротермодинамическая модель программного комплекса «ЗОНА». Не вдаваясь в детали описание модели, укажем, что она получила распространение в России, прежде всего, потому, что была доведена до программной реализации с полным комплектом документации. В то же время и по отношению к модели «ЗОНА» вопросы адекватности ее реальным полям загрязнений в условиях плотной городской застройки и сложной микроме-тереологии остаются открытыми. Вариант модели «ЗОНА» для автомобильного транспорта в настоящее время проходит апробацию в Москве. Известны и другие модели переноса, такие как модель А. П. Курковского, модель фирмы «ИНДИК» (Швеция) и т. п. Их адекватность реальной городской ситуации остается пока недоказанной.

Интерполяционные модели, как уже указывалось выше, в качестве исходных данных используют реальные значения концентраций примесей в заданных точках.

Значения концентрации примесей между заданными точками вычисляются по формулам интерполяции. Чаще других используется линейная интерполяция:

(2.3)

где f(n) - значение функции в точке n, l - расстояние между исходными точками, f(n + l) - значение функции в другой исходной точке,

f(n + x) - значение функции в точке, отстоящей на расстояние х от точки n.

Средняя квадратичная ошибка линейной интерполяции определяется формулой.

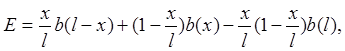(2.4)

где b(l) - структурная функция рассматриваемого параметра:

 Скачать реферат