Выбор основных параметров, расчет и конструирование тепловозов

Для обеспечения равенства нагрузок от кузова между всеми колесными парами локомотива расположим точки его опирания на тележки на одинаковом расстоянии от центра тяжести надтележечного строения (lо=5,15м):

Lт1 = lцт - lо = 9,80 – 5,15 = 4,65 м;

Lт2 = lцт + lо = 9,80 + 5,15 = 14,95 м;

7. Определение Коэффициента использования

сцепного веса локомотива

При движени

и тепловоза в режиме тяги фактический вертикальные нагрузки от колёсных пар на рельсы оказываются различными по величине. Одни колёсные пары догружаются, а другие разгружаются силами ∆П, возникновение которых обусловлено кинематическими особенностями конструкции экипажа.

Поэтому в практике проектирования в качестве одного из критериев оценки тяговых свойств локомотива принято понятие — использование сцепного веса, оцениваемое коэффициентом η:

где ∆Пмакс – величина максимальной разгрузки оси колесной пары.

Взаимодействие колеса и рельса

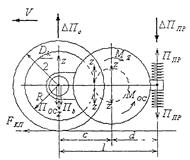
Рис. 9

Рассматривая схему сил и моментов, приведенную на рис.9, определим величину ∆По и ∆Ппр.

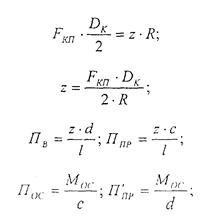
С учетом того, что Мя = Мос, то:

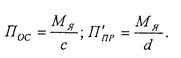
Находим величины сил ∆П0 и ∆Ппр

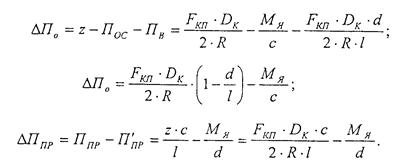
Произведем оценку величины этих реакций. Если принять величину силы тяги, развиваемой одной колесной пары Fкп=70 кН, а диаметр колеса Dk=1,05 м, то величина вращающего момента на валу ТЭД составит:

где i=4,41 – передаточное отношение тягового редуктора, ηдв=0,99 – кпд ТЭД.

Учитывая величины геометрических параметров передачи R=0,374 м, l=0,92 м, с=0,469 м, d=0,451 м, получаем:

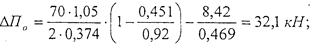
Величина ∆П для экипажей различной конструкции определяется по-разному. В нашем случае используются двухступенчатое рессорное подвешивание. Рассмотрим, как это отразиться на изменении тяговых свойств локомотива. Как и ранее на колеса локомотива действует сила ∆По=0,57Fк. Но теперь, поскольку кузов и тележки локомотива жестко не связаны, то у них появляется возможность получения дополнительного прогиба рессор и поворота относительно друг друга.

Схема определения сил, вызывающих перераспределение нагрузок между колесными парами шестиосного экипажа с двухступенчатым рессорным подвешиванием.

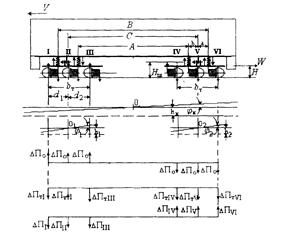
Рис.10

Определяем деформации пружин первой и второй ступени рессорного подвешивания:

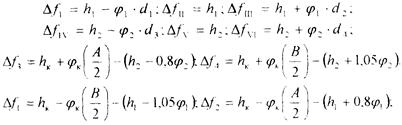
Обозначив жб=1883 Н/мм – жесткость буксового подвешивания колесных пар с учетом жесткости буксовых поводков и гасителей колебаний; жк – жесткость одной пары боковых опор кузова тепловоза, находим величины изменения нагрузок на упругие элементы 1-ой и 2-ой ступеней рессорного подвешивания.

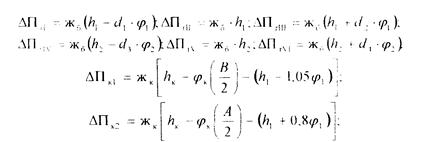
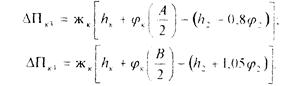
Для определения значений действующих сил составляем уравнения равновесия.

Для первой тележки:

Для второй тележки:

Для кузова:

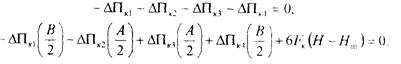
Поскольку локомотив симметричен и d1=d2=d3=d4, то hk=0; h1=h2 и φ1=φ2. Таким образом, система из шести уравнений приводится к трем с тремя неизвестными h1, φ1 и φк.

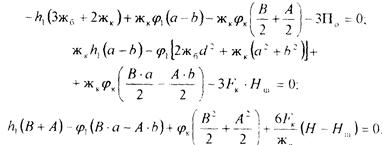
Принимая: Fk=70 кН; жб=1870 н/мм; жк=10920 н/мм; а=1050 мм; b=800 мм; Н=1050 мм; Нш=1135 мм, геометрические параметры экипажа А=3,45 м; В=10,85 м; С=7,15 м; Н=1,05 м; L=8,97 м.

находим:

h1=-h2=-2,463·10-4;

φ1=φ2=-9,56·10-8Fk=-6,69·10-3 рад;

φк=3,98·10-8 Fk=2,8·10-3 рад.

Рассчитываем величины дополнительных усилий на оси колесных пар:

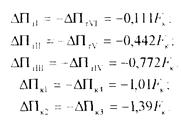
Результирующие величины нагрузок на оси колесных пар будут равны:

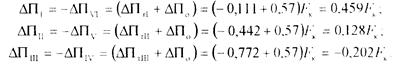
Таким образом, наиболее разгруженной колесной парой является первая по ходу движения тепловоза. Величина коэффициента использования сцепного веса составляет:

η=1 – 0,459·ψ=1 – 0,459·0,3=0,86

8. ГЕОМЕТРИЧЕСКОЕ ВПИСЫВАНИЕ ЭКИПАЖА В КРИВУЮ

При исследовании движения локомотива в кривых приходится решать ряд чисто геометрических задач. Прежде всего необходимо определить, вписывается ли экипаж проектируемого тепловоза в кривую заданного радиуса.

Для решения указанной задачи необходимо прежде всего рассмотреть геометрические соотношения между размерами рельсовой колеи и локомотивного экипажа. Правила технической эксплуатации устанавливают, что при укладке рельсов в кривых, радиус которых меньше 350 м, уширение колеи δ составляет 10 мм, а при радиусе менее 300 м – δ=15 мм.

Для упрощения чертежа на нем изображаются лишь внутренние грани головок рельсов. Расстояние между ними принимается равным суммарному зазору между гребнями бандажей и головками рельсов в кривой, радиус которой менее 300 м, т.е. 29 мм. Соответственно и экипаж локомотива изображается в виде одной линии. Точки на этой линии изображают оси колесных пар, а расстояния от этих точек до кривых, представляют собой зазоры между гребнями колесных пар и головками рельсов. Поэтому крайние колесные пары трехосной тележки прижаты к головкам рельсов, а внутренняя колесная пара имеет относительно них зазор. Для того, чтобы этот зазор можно было измерить непосредственно в мм, при вычерчивании база тележки уменьшается в n раз, а радиус кривой в n2 раз.

Точные значения могут быть получены, если выбрать разные, не связанные друг с другом масштабы my и mx. При этом окружность, изображающая рельс, преобразуется в эллипс, который на участке, необходимом для вписывания локомотива, с большой точностью может быть заменен параболой.

Уравнение параболы, изображающей на чертеже наружный рельс:

.

При построении принимаем масштабы my=1:1, mx=1:100.

Заданный радиус кривой: , получаем:

Подставляя в это выражение величину Х, получим координаты параболы. Если эту параболу сдвинуть параллельно самой себе на 29мм, получим изображение внутреннего рельса. Координаты парабол наружного и внутреннего рельсов представлены в табл.8.

 Скачать реферат