Информационные технологии как средство формирования пространственного воображения школьников при изучении курса стереометрии

б). Задачи на установление числа осей (плоскостей, центров) симметрии.

Пример 1. Найти множество осей симметрии у двух данных точек М и Р на плоскости и в пространстве.

Пример 2. Сколько плоскостей симметрии имеет а) куб, б) цилиндр?

Пример 3. Приведите пример фигуры, имеющей более одного центра симметрии.

в). Задачи на построение осей (центров, плоскостей) симметрии или фигур и

меющих оси (центры, плоскости) симметрии.

Пример 1. Начертите два угла, таких, что один из них может быть получен из другого с помощью центральной симметрии.

Пример 2. Отметьте три точки А, В, С. Дополните это множество четвертой точкой D так, чтобы фигура Ф = {A, B, C, D} имела а) центр симметрии; б) ось симметрии. Рассмотрите все возможные случаи.

Пример 3. Будет ли фигура, являющаяся объединением полосы и прямой, не принадлежащей ей, иметь центр симметрии? Рассмотрите все возможные случаи.

г). Задачи на создание новых образов пространственных объектов путем геометрических преобразований исходных.

Пример. В прямоугольнике ABCD мысленно проведите прямую АК (К - середина стороны ВС), представьте, что прямоугольник разрезан по ней и треугольник АВК повернут вокруг точки К так, что ВК и КС совместились. В какую фигуру превратиться прямоугольник?

IV. Упражнения на конструирование и моделирование новых образов геометрических объектов

Задания данной группы предполагают выполнение мысленного или графического реконструирования и моделирования образ пространственных объектов.

Пример. Нарисуйте фигуру, получающуюся в пересечении двух равных цилиндров, оси которых пересекаются под прямым углом?

В процессе решения таких задач осуществляется конструирование качественно новых пространственных образов и новых отношений между ними, формируются и совершенствуются умения мысленно преобразовывать исходный образ по форме, величине, пространственному положению, то есть, их решение требует активного оперирования пространственными образами и высокого уровня развития пространственных представлений и воображения.

Совокупность данных упражнений можно рассматривать как одно из средств развития пространственных представлений учащихся в процессе изучения геометрии.

Методику формирования пространственного образа геометрического объекта при помощи информационных технологий рассмотрим на примере изучения тел вращения.

Первые два занятия были посвящены изучению темы «Цилиндр». Эти уроки проводились в соответствии с программой, но на каждом уроке использовалась презентация по данной теме. На них были изучены основные понятия и определения, связанные с цилиндром, выведены формулы для вычисления площадей боковой и полной поверхностей цилиндра; рассмотрены типовые и более сложные задачи по изучаемой теме.

Далее в течение четырех уроков изучалась тема «Конус». Обучение происходило по той же схеме, что и тема «Цилиндр», а так же здесь был изучен усеченный конус и все определения и формулы, связанные с ним. Были решены задачи, как простейшие, так и более сложные.

После чего изучалась тема «Сфера. Шар» (4 часа).

В процессе изучения тем «Цилиндр», «Конус» и «Сфера. Шар» нам удалось охватить весь объем теоретической информации. Нами были рассмотрены и отработаны задания на отработку основных умений и навыков, которые являются основными в процессе формирования пространственного воображения. При решении упражнений возникшие затруднения сразу устранялись по мере их возникновения и решались подобные задания на закрепление пройденного материала. Они были достаточно интересны и разнообразны по своему содержанию, отличались новизной формулировок, а также тем, что необходимо было логически мыслить при поиске ответа на поставленный вопрос. На каждом занятие были использованы информационные технологии. Занятия дали положительный результат по формированию умений:

сопоставлять различные изображения образа геометрической конфигурации (оперировать различной наглядностью);

анализировать образ геометрической конфигурации;

синтезировать образ геометрической конфигурации;

вычленять форму образа геометрического объекта;

определять взаимное расположение данного образа геометрического объекта относительно других образов;

определять взаимное расположение отдельных элементов образа геометрического объекта;

конструировать образы новых геометрических конфигураций и воспроизводить их с помощью модели, рисунка, чертежа или словесного описания.

Для сравнения результатов констатирующего среза по формированию пространственного воображения был проведен контрольный срез. Ему посвящен следующий параграф.

Контрольный срез

Для выявления уровня сформированности вышеперечисленных умений с учащимися был проведен контрольный срез и сопоставлен с констатирующим срезом. Контрольный срез также проводился в двух группах. Цель контрольного среза – проверить уровень сформированности пространственного воображения учащихся по сравнению с констатирующим срезом. Кроме того, по результатам решения заданий контрольного среза можно было судить об уровнях сформированности умений работать пространственными фигурами. Все задания объединяла общая цель – сформировать пространственное воображение учащихся с использованием информационных технологий при изучении стереометрии. В срезе содержалось семь заданий, направленных на выявление уровня сформированности пространственного воображения школьников 10 – 11-х классов. Рассмотрим задания одного из вариантов.

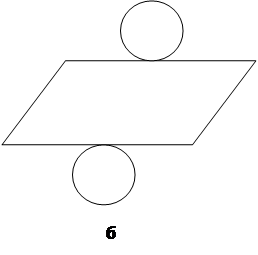
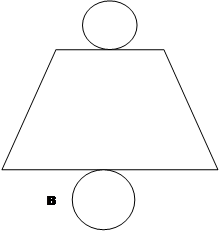
1. Какие из предложенных на рисунке фигур являются разверткой цилиндра? (Ответ а), б))

2. На поверхности шара даны три точки, кратчайшее расстояние между которыми равно 6см. Определить площадь сечения, проходящего через эти три точки.

3. Диагонали ромба 15 см и 20 см. Шаровая поверхность касается всех его сторон. Радиус шара 10 см. Найдите расстояние от центра шара до плоскости ромба.

4. Какая фигура образуется при вращении вокруг оси (достроить). Вычислите полную поверхность тела вращения, которое получается в результате вращения вокруг его стороны АС, если АС = 8см, ВС = 5см.

5. В конусе даны радиус основания R и высота H. В него вписана правильная треугольная призма, у которой боковые грани – квадраты. Найдите ребро призмы.

6. Образующая конуса, равная 12 см, наклонена к плоскости основания под углом . Найдите площадь основания конуса, если . ()