Сравнительный анализ методик преобразований Галилея в курсе общей физики и в курсе элементарной физики

,

где – координата первого тела в любой, произвольный момент времени.

Записывают уравнение движения для второго тела:

; ;

; ; ; .

Уравнение координаты для второго тела:

,

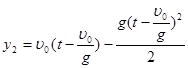где – координата второго тела в любой, произвольный момент времени, – время движения первого тела до момента бросания второго тела.

В момент встречи тел в полете их координаты равны, т. е. (условие встречи).

Приравняв координаты и решив полученное уравнение относительно , получают: – время, прошедшее от момента бросания первого тела до встречи его со вторым.

Так как от момента бросания первого тела до момента бросания второго тела прошло время , то ответ на вопрос задачи такой: , т. е. время, прошедшее до момента встречи тел от момента бросания второго тела равно .

Решение 2. За начало отсчета времени выбирают момент бросания второго тела (рис. 2), остальные условия те же, что и в первом решении.

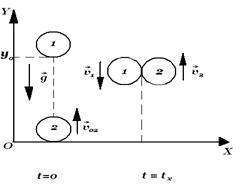
Рис. 2

Записывают уравнение движения для первого тела:

; ; ; ; ; .

Уравнение координаты для первого тела:

,

где – координата первого тела в любой, произвольный момент времени.

Записывают уравнение движения для второго тела:

; ; ; ; .

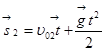Уравнение координаты для второго тела:

,

где – координата в любой, произвольный момент времени.

Решают систему уравнений при условии, что (условие встречи) и в данном решении по сравнению с первым сразу получают ответ на вопрос задачи: .

Решение 3. Выбирают систему отсчета так, чтобы телом отсчета было второе тело, которое еще находится на Земле. Совместим начало отсчета координаты со вторым телом, ось направим вверх. За начало отсчета времени принимают момент бросания второго тела. Первое тело движется относительно второго тела в этой системе отсчета равномерно и прямолинейно. Первоначальное расстояние первого тела от начала координат . Двигаясь равномерно и прямолинейно в этой системе отсчета со скоростью , первое тело пройдет это расстояние за время

.

В этом случае задачу решают в одно действие, в то время как в первом решении – в четыре действия, во втором – в три. Следовательно, последнее решение наиболее рационально. Это первый вывод, который можно сделать на основании проведенных решений задачи.

Второй, наиболее важный, вывод: характер движения тела зависит от выбора системы отсчета: в первых двух решениях мы имели дело с равноускоренным прямолинейным движением тел, в третьем решении первое тело двигалось относительно второго равномерно и прямолинейно.

Полезны также задачи для случая, когда векторы скорости направлены под углом друг к другу.

Завершая изучение кинематики, целесообразно предложить учащимся обобщить материал об относительности в виде таблицы (табл. 2).

Эту таблицу школьники дополняют при изучении динамики и законов сохранения.

Преобразования Галилея

Преобразования Галилея – это уравнения, связывающие координаты и время некоторого события в двух инерциальных системах отсчета. Событие определяется местом, где оно произошло (координаты ), и моментом времени , когда произошло событие. Событие полностью определено, если заданы четыре числа: – координаты события.