Исторические экскурсы в курсе алгебры 7 класса как средство развития познавательного интереса

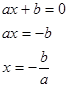
Уравнение вида, где -числа, причем называется линейным уравнением с

2 переменными и (или с 2 неизвестными и ).

Решением уравнения называется всякую пару чисел , которая удовлетворяет этому уравнению, т.е. обращает равенство с переменными в верное числовое равенство. Таких решений бесконечно много.

Графиком любого линейного уравнения является прямая.

4. Исторический экскурс об уравнениях.

Записывать и решать уравнения начали арабы в первом тысячелетии нашей эры. До тех пор решение задач было исключительно арифметическим - из многих действий. В тот момент, когда появилась блестящая идея находить неизвестное, записав соотношения, которыми оно связано с известными величинами, и затем выразив это неизвестное из этих соотношений, родилась алгебра. Слово "алгебра" - арабского происхождения; великий ученый арабского мира Аль-Хорезми называл перенесение членов из одной части равенства в другую так, чтобы все они стали положительными, словом "аль-джебр" (восстановление), а словом "аль-мукабала" (противопоставление), исчезнувшим ныне из математического языка, называлось приведение подобных членов, в результате которого в уравнении для каждой степени неизвестного остается только один положительный член.

В те времена не было еще общепринятых теперь обозначений переменных буквами, а действий - знаками. Уравнения записывались словами. Но и в такой "словесной форме" уравнения существенно облегчали жизнь. Арифметика (как и классическая геометрия) не знала общих подходов к решению задач, но для каждой новой задачи нужно было подбирать новое решение.

Применение уравнений упрощает решение задач; но самое замечательное то, что одним и тем же уравнением могут описываться совершенно разные ситуации. Научившись решать некоторый тип уравнений, можно тем самым справиться с целыми классами задач, описывающихся уравнениями этого типа.

Самостоятельная работа учащихся: Среди решений уравнения х + 3у - 20 = 0 найдите такую пару, которая состоит:

а) из двух одинаковых чисел;

б) из двух таких чисел, 1 из которых в 2 раза больше другого.

5. Закрепление полученных знаний.

5.1 Выполнение № 803 (у доски):

а) да, является линейным уравнением;

б) да, является линейным заданное уравнение.

5.2 Выполнение № 804 (у доски):

а) потому что задействована только одна переменная;

б) потому что в нем есть одночлен 2 степени.

5.3 Выполнение № 805 (с комментированием):

а) нет; б) да; в) нет; г) нет.

5.4 Выполнение № 807 (самостоятельно):

а) (6;

2), (0; 20), (4;

8); б) (2; 0), (2,5; 2,5).

5.5 Выполнение № 810 (с комментированием):

М: 5+14-7=0 - неверно, значит, точка М не принадлежит графику уравнения

N: 0+7-7=0 - верно, значит, точка N принадлежит графику уравнения

К: 7+0-7=0 - верно, значит, точка К принадлежит графику уравнения

L: 2+6-7=0 - неверно, значит, точка L не принадлежит графику уравнения

5.6 Выполнение № 811 (у доски):

5.7 Выполнение № 813 (а) (самостоятельно):

Ответ: 3.

5.8 Выполнение № 827 (а) (у доски):

а)

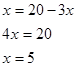
Ответ: (5;5).

6. Д/з № 804 (б, г), № 806, № 808 (б, г), № 814 (б).

7. Итог урока.

Анализ урока.

Тип урока - урок изучения нового материала. Цели и задачи урока: проверить знания, умения, навыки по теме "Координатная плоскость"; познакомить учащихся с линейным уравнением с двумя переменными и его графиком; развивать математическую речь, активность, внимание, навыки самостоятельности; воспитывать аккуратность, интерес к предмету. Цели и задачи урока решены. Использовался исторический экскурс об уравнениях. В качестве дополнительного домашнего задания учащимся была предложена самостоятельная работа. Исторический материал заинтересовал учащихся.

Пробный урок алгебры в 7 классе, МОУ "Кыласовская СОШ"

Тема: Линейная функция и ее график

Цели: - познакомить учащихся с линейной функцией и ее графиком;

развивать математическую речь, активность, внимание, навыки

самостоятельности;

воспитывать аккуратность, интерес к предмету.

Оборудование: портрет Пьера Ферма.

Ход урока:

1. Сообщение темы и целей урока.

2. Работа по теме урока.

Линейное уравнение с 2 переменными и всегда можно преобразовать к виду , где -числа (коэффициенты), причем .