Исторические экскурсы в курсе алгебры 7 класса как средство развития познавательного интереса

Самостоятельная работа учащихся: найти энциклопедическую справку о Евклиде; найти 2 задачи Евклида и решить их; что называют "пифагоровыми тройками".

4. Закрепление пройденного материала.

4.1 Выполнение задания № 626 (в) (у доски):

в)

4.2 Выполнение задания № 627 (в) (с комментированием):

в) dth=543 height=49 src="images/referats/29013/image002.png">

4.3 Выполнение задания № 628 (в) (самостоятельно):

в)

4.4 Выполнение задания № 629 (в) (самостоятельно):

в)

Проверка: кто первым решит, записывает ответ на доску.

4.5 Выполнение задания № 634 (а, в) (дополнительно):

а)

в)

5. Д/з № 630 (в), № 631 (в), № 632 (в), № 633 (в).

6. Итог урока.

Анализ урока.

Тип урока - урок закрепления. Цели и задачи урока: повторить формулы сокращенного умножения; отрабатывать навыки рациональных вычислений; развивать математическую речь, активность, внимание, навыки самостоятельности; воспитывать аккуратность, интерес к предмету. Цели и задачи решены. На уроке использовался исторический экскурс о Евклиде. Историческая справка заинтересовала учащихся.

Пробный урок алгебры в 7 классе, МОУ "Кыласовская СОШ"

Тема: Тождества

Цели: - познакомить учащихся с тождествами;

отрабатывать навыки рациональных вычислений;

развивать математическую речь, активность, внимание, навыки

самостоятельности;

воспитывать аккуратность, интерес к предмету.

Оборудование: портрет Франсуа Виет де ла Биготье.

Ход урока:

1. Сообщение темы и целей урока.

2. Работа по теме урока.

Тождество - это равенство, верное при любых допустимых значениях, входящих в его состав переменных.

Исторический экскурс о Франсуа Виете.

Франсуа Виет де ла Биготье (1540-1603)

Франсуа Виет был юристом и советником у французских королей Генриха III и Генриха IV. Математикой он занимался "в свободное от работы время". Виет внес значительный вклад во все области современной ему математики, но особенно велики его заслуги в развитии алгебры: он был первым, кто начал употреблять алгебраическую символику. Впрочем, его символика не получила широкого распространения. Современная алгебраическая символика в основном ведет свое начало от "Рассуждения о методе" Р. Декарта (1637 г.). В одной из его первых книг "Математические таблицы", опубликованной в 1579 году в Париже, автор говорит о преимуществах десятичных дробей при вычислениях и сам широко их использует.

Франсуа Виет - выдающийся французский математик. Его называют "отцом алгебры". Каждому школьнику известно это имя по знаменитой теореме Виета. В сочинениях Виета подводится своеобразный итог математики эпохи Возрождения. Главным трудом его жизни было сочинение по новой алгебре "Введение в искусство анализа". Виет был первым европейским математиком, который решал числовые уравнения приближенным путем. Его научные открытия легли в основу развития новой науки - аналитической геометрии. Виету принадлежат разложения тригонометрических функций кратных дуг посредством последовательного применения формул для синуса и косинуса сумм двух углов. Труды Виета привели к тому, что алгебра сформировалась как наука о решении уравнений.

Самостоятельная работа учащихся: найти задачу Франсуа Виета и решить ее; что называют тригонометрическими функциями, аналитической геометрией.

4. Закрепление полученных знаний.

4.1 Выполнение № 707 (а, б) (у доски):

а) (да); б) (да).

4.2 Выполнение № 708 (а, б) (с комментированием):

а) является тожеством; б) является тожеством.

4.3 Выполнение № 709 (а, б) (самостоятельно):

а) является тождеством; б) является тождеством.

4.4 Выполнение № 710 (а, б) (с комментированием):

а) переместительный закон сложения;

б) сочетательный закон сложения.

4.5 Выполнение № 712 (а, б) (у доски):

а) 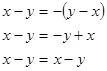б)

5. Д/з № 707-712 (в, г).

6. Итог урока.

Анализ урока.

Тип урока - урок изучения нового материала. Цели и задачи урока: - познакомить учащихся с тождествами; отрабатывать навыки рациональных вычислений; развивать математическую речь, активность, внимание, навыки самостоятельности; воспитывать аккуратность, интерес к предмету. Цели и задачи урока решены. На уроке использовался исторический экскурс о Франсуа Виете. В качестве дополнительного домашнего задания учащимся была предложена самостоятельная работа. Исторический материал заинтересовал учащихся.

Пробный урок алгебры в 7 классе, МОУ "Кыласовская СОШ"

Тема: Координатная плоскость

Цели: - повторить понятие координатной прямой, координаты точки, виды

числовых промежутков;

развивать математическую речь, активность, внимание, навыки

самостоятельности;

воспитывать аккуратность, интерес к предмету.

Оборудование: портрет Рене Декарта.

Ход урока:

1. Подготовка учащихся к восприятию нового материала (фронтальная работа с классом).

1.1 Что называют координатной прямой?

Координатной прямой называют прямую, на которой выбрано начало отсчета, единичный отрезок и указано направление.

1.2 Что называют координатой точки?

Число, определяющее положение точки на прямой, называется координатой точки.

1.3 Какие виды числовых промежутков вы знаете?

Числовые промежутки: луч, открытый луч, интервал, отрезок, полуинтервал.

2. Сообщение темы и целей урока.

3. Изучение нового материала.

Проведем 2 взаимно-перпендикулярные координатные прямые и будем считать началом отсчета на обеих прямых точку их пересечения - точку О. тем самым на плоскости задана прямоугольная система координат, которая превращает обычную плоскость в координатную.