Применение решебников в учебной практике

mv2c/R = mgcosα.

Как видно из рисунка, cosα = (R – h)/R. Тогда

mv2c = mg(R-h). (4)

Уравнения (3) и (4) содержат скорость и высоту, относящиеся к одной и той же точке С, и образуют систему, совместное решение которой позволяет найти

h = R/3 = 0,3 м.»

Мы привели дословное текстовое описание решения задачи. Как видим, оно отличается детальным анализом физической ситу

ации. Здесь приняты во внимание такие подробности, как точечные размеры груза (тем самым исключена необходимость учитывать расход энергии на вращение твёрдого тела). Здесь подчеркнуто отсутствие трения (отмечена идеальная гладкость поверхности сферы). Не упущен вопрос о начальном моменте (пренебрежимо малая начальная скорость тела). Прослежена картина изменения скорости и нормального ускорения. Приведено обоснование рабочей записи закона сохранения энергии – в неё не включена работа силы нормального давления. После такого детального анализа решение задачи не представляет значительной трудности, практически с этого момента идёт процесс письменного оформления решения.

Приведём из того же пособия ещё один пример подробного анализа физической ситуации, соответствующей сюжету задачи, а также детального обоснования всех действий, составляющих её решение.

Задача 4 (2.5.Н5). На наклонной плоскости находится груз т1 = 5 кг, связанный нитью, перекинутой через блок, с другим грузом т2 =2 кг (рис. 13). Коэффициент трения между первым грузом и плоскостью k= 0,1; угол наклона плоскости к горизонту α = 37°. Определить ускорения грузов. При каких значениях т2 система будет находиться в равновесии?

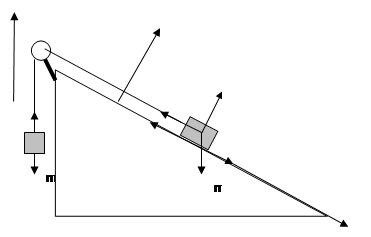Анализ. В задаче рассматриваются два тела, связанные нитью и совершающие поступательное движение. Если нить, как всегда, считать нерастяжимой, то ускорения этих тел равны по модулю: а1 = а2.

На тело массы m1 действуют сила тяжести m1g, сила нормальной реакции N наклонной плоскости, сила натяжения Т1 нити и сила трения fТР. Сила трения направлена в сторону, противоположную скорости тела; если же направление движения системы неизвестно, то нельзя указать направление силы трения. Но так как сила трения не может изменить направление движения на противоположное, то следует определить сначала направление движения при отсутствии трения, а затем уже решать задачу с учетом силы трения. Второй закон Ньютона для первого тела без учета силы трения имеет вид

m1a1 =m1g +T1+N. (1)

На тело m2 действуют только сила тяжести m2g и сила натяжения Т2 нити:

m2a2 = m2g + T2. (2)

Вводя оси координат и заменяя векторные уравнения (1) и (2) скалярными равенствами, получим систему уравнений, решение которой позволит определить направление ускорения а1. Поскольку тела не имели начальной скорости, мгновенная скорость каждого из тел совпадает по направлению с его ускорением, следовательно, направление силы трения, действующей на тело m1 , будет известно. После этого можно решать задачу уже с учетом силы трения. При этом в уравнение (1) надо ввести в правую часть силу трения, уравнение (2), очевидно, не изменится. При рассмотрении условий равновесия следует повторить все рассуждения, учитывая, что в этом случае

a1 = a2=0 (3)

Решение. Для замены векторных уравнений (1) и (2) скалярными введем для описания движения тела m1 оси Х и У, тела m2 - ось η (рис. 13). Учитывая, что вследствие невесомости нити и блока, Т1 = Т2, получаем:

m1a1 x= m1gsinα—T, m2a2η = T - m2g , a1 x = a2η (4)

После совместного решения уравнений (4) получаем

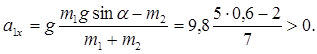
Проекция вектора а на ось Х положительна, это значит, что тело m1 движется вниз по наклонной плоскости, следовательно, сила трения направлена вверх по наклонной плоскости. Можно, не возвращаясь к векторным уравнениям, ввести силу трения в первое из уравнений (4). При этом следует учесть, что

a1 x = a2η= a, fTP=-fTPx= - kN.

Тогда

m1a= m1gsinα—T-kN, m2a = T - m2g.

Силу нормальной реакции N найдем из уравнения (1), записанного в скалярном виде для проекций на ось Y:

a1y = 0, 0 = N - m1gcosα,

откуда

N = m1gcosα.

Окончательно

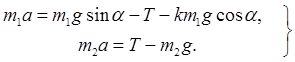(5)

Совместное решение системы (5) дает

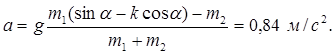
Условия равновесия, соответствующие равенству нулю результирующей силы, действующей на каждое тело, зависят, очевидно, от наличия силы трения и ее направления. Если трения нет, то, как следует из решения системы (4),

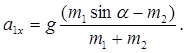
В условиях равновесия a1 x =0 и т2 = т2* = т1 sinα = 3 кг. Если т2 < т2* , то a1 x > 0—тело т1 движется вниз по наклонной плоскости; если m2> т2* , то a1 x < 0—тело т1 движется вверх по наклонной плоскости. В условиях равновесия сила трения является силой трения покоя и ее направление противоположно направлению возможного движения тела т1. В первом случае (т2 < т2*) сила трения направлена вверх по наклонной плоскости и систему (4) с учетом того, что a1 x = a2η=0, можно переписать в виде

0= m1gsinα - T -fTP, 0 = T-m2g, (6)

откуда

m2= m1sinα - fTP/g. (7)

Во втором случае (m2> т2* т) сила трения направлена вниз по наклонной плоскости и уравнения (6) примут вид

0= m1sinα - T + fTP, 0 = T - m2g, (8)

откуда

m2= m1sinα + fTP/g.

В обоих случаях сила трения покоя fTP ≤ kN = km1gcosα. С учетом этого неравенства выражения (7) и (8) примут вид

Легко видеть, что первое неравенство имеет смысл только когда sinα>kcosα. Оба неравенства не противоречат друг другу, и равновесие имеет место при 2,6 кг ≤m2 ≤3,4 кг.

Предельным значениям массы т2 соответствует наибольшая сила трения покоя

(f тр.макс = kN). Если т2 =2,6 кг или m2=3,4 кг, то при малейшем толчке (в первом случае—вниз, во втором—вверх) начнется движение системы. В обоих случаях движение будет равномерным.

Задача решена аналитическим методом, её описание содержит дополнительный материал, который лишь на первый взгляд делает решение излишне громоздким. На самом деле это хорошая иллюстрация методологии физики, как науки, при рассмотрении любой физической ситуации. Пользуясь такими пояснениями можно существенно повысить точность и обоснованность ответа, углубить уровень усвоения теоретического материала и приобрести навыки решения задач повышенной сложности.

Запись условия задачи следует завершать после её анализа

Как видно из приведённых примеров, авторы пособий по решению задач по разному подходят к рассматриваемой проблеме. Так например, в предисловии цитированного выше решебника В.Б.Лабковского выделены пять составных частей (этапов) решения задач, перечень которых нам представляется не только не идеальным, но во многом ошибочным.