Применение решебников в учебной практике

Этот пример приведен с целью обоснования следующего тезиса - в решебнике при самом подробном описании задачи не бывает избыточной информации. Именно в этом и должно состоять одно из главных требований к решебнику – здесь все должно быть обосновано и учтено, операции с понятиями обозначены, аргументы и альтернативы приведены полностью. В обычной практике мы пользуемся сокращенными силлогизмами,

опускаем всё то, что кажется нам тривиальным или несущественным в данных условиях. Тем самым мы ускоряем процесс изложение материала, но – и это очень важно – не ускоряем процесс мышления. В ходе мыслительных операций мы эти суждения и посылки отслеживаем и оцениваем, существенные мы оставляем и используем в устном или письменном решении. Заметим для себя, что устное объяснение мы всегда даём более подробно, чем письменное. Всё из тех же соображений экономии времени. Но, выиграв во времени, мы рискуем проиграть в точности решения, поскольку не учли какие-то сопутствующие явления и/или неправильно оценили их вклад конечные выводы.

Поэтому на этапе обучения сжатое (формульное) описание решений, характерное для большинства «решебников», не обосновано с позиции углубления теоретических знаний. Оно также непродуктивно с позиции развивающего обучения, поскольку процедура обоснования – это упражнение в мышлении, а отсутствие таковых препятствует развитию логики и интеллекта в целом. Только аналитическое по структуре рассуждений, построенное на строгой силлогистической основе, очищенное от излишних действий решение становится «пригодным к употреблению» - накладываясь на предыдущий опыт обучаемого, оно способствует очищению его индивидуальных алгоритмов от лишних деталей, создает новые («валентные») связи ассоциативного типа.

2. Решению должен предшествовать анализ сюжета задачи

Решение, не содержащее текстового пояснения и состоящее только из формул и математических действий, обучает сугубо ремесленным навыкам и приёмам. В её основе лежит ошибочный методический приём, который можно назвать так - «есть такая формула».

В качестве иллюстраций рассмотрим авторские варианты из учебных пособий нескольких авторов.

Задача 2. (№58 - Л[1]). «Маленький шарик скатывается с полусферы радиусом R. На какой высоте он оторвётся от сферы?

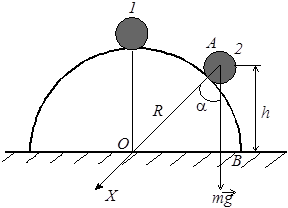Решение. Пусть шарик отрывается от сферы в точке 2. Значит, в этой точке исчезает реакция опоры и остаётся только сила тяжести mg. Второй закон Ньютона имеет вид

Ось Х , как всегда при вращательном движении, направляем к центру траектории и проецируем уравнение на эту ось:

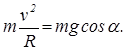
Из треугольника ОАВ

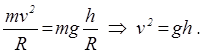
Из закона сохранения механической энергии

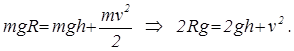
Решаем совместно два уравнения:

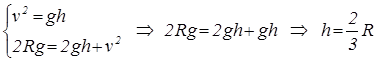
Ответ: »

Задача решена, ответ получен и на первый взгляд решение правильное. Однако отсутствует анализ физической ситуации и многие из возможных обстоятельств не учтены. Так например, для катящегося шарика необходимо учесть энергию вращения. Слабо прописаны параметры движения в момент отрыва. Краткость изложения не делает решение более понятным, и уж тем более не учит обстоятельности.

Эти недостатки базируются на следующей особенности мыслительного процесса, сопутствующего решению задачи. Мы здесь умышленно выделяем мыслительные операции, поскольку они протекают с очень высокой скоростью, и не всегда выливаются в устную и, тем более, письменную форму. Так вот, в ходе мысленного поиска ответа неизбежно затрагивается дополнительно обширный материал курса физики, как оказывается в дальнейшем, не играющий существенной роли в формировании ответа. Этот материал уместно отнести в общий базис задачи. Если этот базис принимается к обсуждению в ходе анализа условия задачи, то вероятность ошибки значительно уменьшается. В задаче №86 этого пособия, где также нет анализа физических процессов, вновь катятся шары, а в законе сохранения механической энергии записаны кинетические энергии только для поступательного движения.

Сравним теперь это решение с другим вариантом объяснения подобной же задачи.

Задача 3. (3.6. – Н). «С вершины идеально гладкой сферы соскальзывает небольшой груз. С какой высоты h , считая от вершины, груз сорвётся со сферы? Радиус сферы R =90 см.

Анализ. Груз, который, очевидно, можно считать точечным телом, до некоторой точки – точки отрыва – движется по дуге окружности радиуса R. На груз во время его движения по сфере действует сила тяжести mg и сила нормального давления со стороны сферы. Уравнение второго закона Ньютона для этой части траектории имеет вид

(1)

Проекции этих сил на направление, нормальное к траектории, сообщают телу нормальное ускорение an = v2/R, где v – мгновенная ( и, очевидно, непрерывно возрастающая) скорость тела. В точке С отрыва прекращается взаимодействие между движущимся телом и поверхностью сферы и, следовательно, сила давления тела на сферу и соответственно сила реакции сферы N обращаются в нуль. (Начиная с этой точки тело движется только под действием силы тяжести и траектория его будет зависеть от модуля и направления скорости тела в точке отрыва от сферы.) Таким образом, в этой точке нормальное ускорение, однозначно зависящее от скорости, сообщает телу только проекция силы тяжести. Для того, чтобы определить высоту, на которой находится точка отрыва, надо найти связь скорости тела при его движении по сфере с его координатами, в частности с высотой. Такую связь можно найти, зная законы изменения со временем координат и скорости тела. Можно это сделать и рассматривая движение тела в поле силы тяготения Земли. Поскольку сила нормальной реакции работы не совершает, полная энергия тела остаётся неизменной, т.е.

ΔE = ΔK + ΔU = 0. (2)

Очевидно, что применение закона сохранения энергии к переходу из начального состояния в точку отрыва даст в явном виде связь между скоростью тела и высотой рассматриваемой точки.

Решение. При скольжении груза по сфере потенциальная энергия его изменяется на

ΔU =-mgh,

Где h - искомая высота, отсчитываемая от вершины сферы. Кинетическая энергия тела возрастает на

ΔK = mv2c /2 – mv20/2.

На вершине сферы груз находится в состоянии неустойчивого равновесия и скорость v0, необходимую для начала движения, можно считать пренебрежимо малой. Тогда, подставляя найденные выражения в (2), получаем

-mgh + mv2c/2 = 0 (3)

Чтобы от векторного уравнения (1) перейти к скалярным соотношениям, введём ось Х, направленную вдоль радиуса. Тогда ax = an = v2/R. На основании уравнения (1) mv2/R = mghcosα – N. В точке отрыва от сферы an = v2c/R, N=0, следовательно ,