Организация обобщающего повторения на уроках геометрии в 7 классе

Задачи

1.

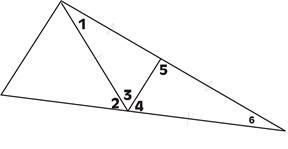
Угол 1=40°; угол 2=80°

Найти углы 3,4,5,6.

(Используются свойства равнобедренного треугольника.)

	>

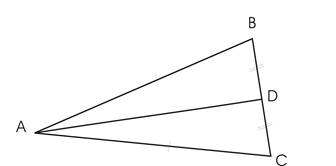PABC=50 см; PABD=30 см

(Используется определение периметра треугольника.)

Найти пары равных треугольников и доказать их равенство.

(Для доказательства равенства треугольников DCF и DEH используются свойство углов при основании равнобедренного треугольника и II признак равенства треугольников; для доказательства равенства треугольников DCH и DEF можно использовать любой из трех признаков.)

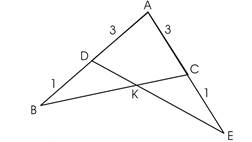
4.

Доказать:

ВС=ЕD; КВ=КЕ

(Используются I и II признаки равенства треугольников.)

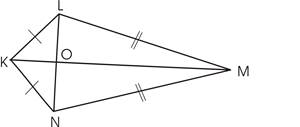5.

(Используется сначала III признак равенства треугольников, затем свойства равнобедренного треугольника, I или II признаки.)

В приложении 1 приводятся задачи, которые также можно использовать на этом этапе урока.

3) Систематизация знаний о признаках равенства

треугольников.

В ходе решения задач по готовым чертежам учащиеся повторили все признаки равенства треугольников. Теперь вместе с учителем они рисуют следующую схему:

Затем учитель предлагает учащимся ответить на вопросы: сколько нужно пар соответственно равных элементов для доказательства равенства треугольников? Достаточно ли двух пар и почему? Нужны ли четыре пары? Существуют ли другие признаки равенства треугольников по трем элементам? Можно ли доказать равенство треугольников по трем углам?

Важно ли, что в I признаке угол лежит между сторонами, а во II признаке оба угла прилежат к стороне?

Последний вопрос приводит к следующим двум задачам:

1. Доказать, что треугольники ABC и A1B1C1 равны, если АВ=А1В1, BC=B1C1 и углы A и A1 равны.

2. Доказать, что треугольники АВС и А1В1C1 равны, если углы A и A1, B и B1, C и С1 равны (задача №174 из учебника).

4) Решение задач (письменно).

В классе учащиеся решают задачу 1; задача 2 задается на дом (т.к. при ее решении используется теорема о сумме углов треугольника, которую учащиеся должны будут повторить к следующему уроку).

Дано: АВ=А1В1

BC=B1C1 и углы A и A1 равны.

Доказать: ∆ABC=∆A1B1C1

Доказательство:

Дополнительные построения: BH ┴ AC, B1H1 ┴ A1C1

1) Рассмотрим прямоугольные треугольники ABH и A1B1H1

По условию AB=A1B1, углы А и А1 равны => ∆ABH=∆A1B1H1 , (по гипотенузе и острому углу) => AH=A1H1, BH=B1H1.

2) Рассмотрим прямоугольные треугольники ∆CBH и ∆C1B1H1.

По условию BC=B1C1,по доказанному BH=B1H1=> ∆CBH=∆C1B1H1 (по гипотенузе и катету) =>CH=C1H1.

3) По доказанному AH =A1H1, CH=C1H1 => AC=A1C1.

4) Рассмотрим треугольники ∆АВС и ∆A1B1C1.

По условию AB=A1B1, BC=B1C1, по доказанному AC=A1C1 => ∆ABC=∆A1B1C1 (по III признаку), что и требовалось доказать.

Если остается время, то учащиеся решают задачу №175 из учебника.

175.

Доказать: ОЕ – биссектриса.

Доказательство:

1) По условию ОА=ОВ, АС=ВО => ОС=ОО.

2) Рассмотрим треугольники ∆АОD и ∆ВОС.

По условию ОА=ОВ, по доказанному ОС=ОD, угол COD – общий => ∆АОD и ∆ВОС (по I признаку) => углы OAD и OBC равны, углы ODA и OCB тоже равны.

3) По доказанному углы OAD и OBC равны => углы EAC и EBD тоже равны.

4) Рассмотрим треугольники ∆АЕС и ∆ВЕС.

По условию АС=ВВ, по доказанному углы ЕАС и ЕВВ равны, углы АСЕ и ВВЕ равны => ∆АЕС=∆ВЕD (по II признаку) => АЕ=ВЕ.

5) Рассмотрим треугольники ∆ОАЕ и ∆ОВЕ.

По условию ОА=ОВ, по доказанному АЕ=ВЕ, ОЕ - общая => ∆ОАЕ=∆ОВЕ (по III признаку) => углы АОЕ и ВОЕ равны => ОЕ - биссектриса угла ХОУ (по определению биссектрисы угла), что и требовалось доказать.

5). Постановка домашнего задания.

Повторить по учебнику п. 30 - 34.

Решить задачи №174 и №177. При решении задачи №174 не пользоваться указанием, данным в учебнике! (Решение, предлагаемое в учебнике, слишком сложное, т.к. задача дана в главе «Треугольники», после изучения которой учащиеся еще не имеют достаточной базы для более простого решения.)

Темой данной работы является одна из важных проблем обучения математике в школе - организация итогового повторения курса геометрии 7 класса. В работе рассмотрены общие принципы организации обобщающего повторения, разработаны уроки обобщающего повторения по темам «Признаки равенства треугольников» и «Соотношения между сторонами и углами треугольника», а также приведена подборка задач, которые можно использовать на данных уроках.