Моделирование нагрева асинхронного двигателя

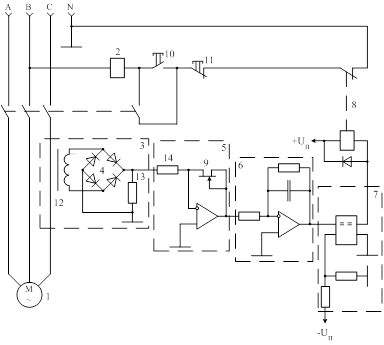
Рисунок 1.5 – Устройство для защиты электродвигателей

В патенте №2192699 описывается устройство для защиты электродвигателя. Принципиальная схема устройства приведена на рисунке 1.6.

Это устройство содержит трансформаторы тока (1, 2, 3), выпрямитель (4), блок (5) контроля перегрузок, блок формирования времятоковой ха

рактеристики, состоящий из теплового имитатора (6) электродвигателя, компаратора (7), и исполнительного реле (8). Здесь так же используется тепловая модель первого порядка.

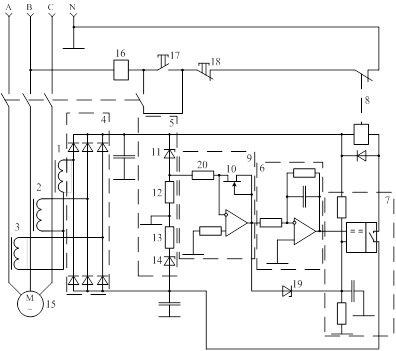
Рисунок 1.6 – Устройство для защиты электродвигателя

2. Выбор и определение параметров тепловой модели асинхронного двигателя

2.1 Выбор тепловой модели

Задача выбора АД по нагреву не требует высокой точности определения температуры меди, которую обеспечивает ЭТС с большим количеством узлов. Поэтому за основу принята модель, представляющая двигатель как два коаксиальных цилиндра [7,8] (см. рисунок 1.4). Основные принципы, на которых базируется модель, рассмотрены в разделе 1.

Данная модель более точно моделирует нагрев двигателя по сравнению с представлением двигателя однородным телом нагрева. В то же время имеется возможность аналитического определения коэффициентов, присутствующих в уравнении (1.20), с достаточной для поставленной задачи точностью.

Перегруппировав неизвестные в уравнениях системы (1.20) получим систему вида:

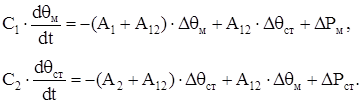(2.1)

Системе уравнений (2.1) соответствует ЭТС, изображенная на рисунке 2.1.

В указанной схеме тепловые сопротивления определяются как величины, обратные соответствующим коэффициентам теплоотдачи.

Таким образом, коэффициенты А1, А12 и А2 возможно определить, приведя эквивалентными преобразованиями тепловую схему замещения асинхронного двигателя к тепловой схеме двухцилиндрической модели.

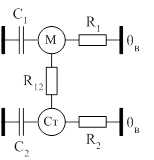
Рисунок 2.1 – ЭТС, соответствующая двухцилиндрической модели двигателя

2.2 Определение коэффициентов теплоотдачи

2.2.1 Аналитическое определение А1, А2, А12

Для определения коэффициентов теплоотдачи рассмотрим упрощенную эквивалентную тепловую схему замещения асинхронного двигателя закрытого исполнения [4,9], (см. рисунок 1.3). Коэффициенты теплоотдачи считаем постоянными, то есть одинаковыми в переходном и установившемся режимах. Следовательно, для их определения можно рассматривать схему (см. рисунок. 1.3) в установившемся режиме (рисунок 2.2), что значительно упрощает решение. Так же введем допущение, что двигатель имеет независимое принудительное охлаждение, то есть коэффициенты теплоотдачи одинаковы при выключенном и включенном двигателе.

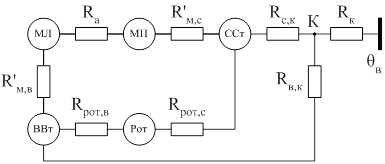
Рисунок 2.2 – Приведенная ЭТС закрытого обдуваемого двигателя для стационарного режима

Система уравнений для этой схемы имеет вид 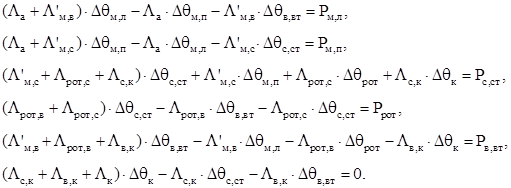[2]:

(2.2)

Так как в схеме (рисунок 2.2) рассмотрены лобовая и пазовая части обмотки в отдельности, а необходимо знать среднюю температуру обмотки, то по правилам эквивалентных преобразований [4], объединим эти источники в один (рисунок 2.3).

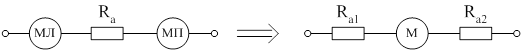
Рисунок 2.3 – Объединение лобовой и пазовой частей обмотки

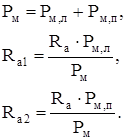
После преобразования (2.3) схема имеет 5 узлов (рисунок 2.4), то есть схеме соответствует система уравнений 5-го порядка.

Объединим сопротивления Ra1 с R'м,в и Ra2 с R'м,с:

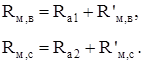(2.4)

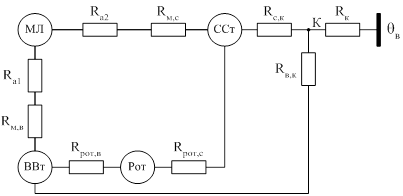
Рисунок 2.4 – ЭТС закрытого обдуваемого двигателя с объединенными пазовой и лобовой частями обмотки

В итоге имеем схему, изображенную на рисунке 2.5 которой соответствует система уравнений (2.5).

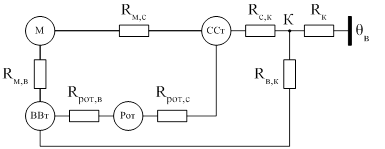
Рисунок 2.5 – Окончательный вид преобразованной ЭТС закрытого обдуваемого двигателя

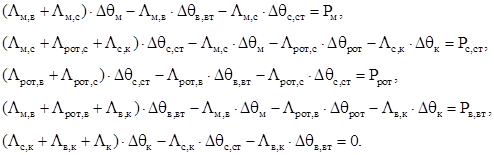(2.5)

Систему уравнений (2.5) необходимо свести к системе уравнений второго порядка, в которой неизвестными выступили бы Δθм и Δθс,ст. Для сокращения записи выражений введем замену:

Подставив в (2.5) выражения (2.6), получим:

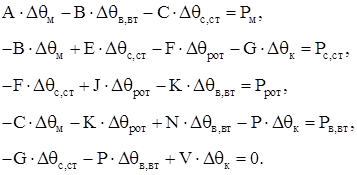(2.7)

Пренебрежем механическими и добавочными потерями (Pв,вт=0), так как их величина мала по сравнению с основными потерями (потери в меди, стали, роторе) и, как следствие, они незначительно влияют на превышение температуры меди и стали.

Для того чтобы понизить порядок системы (2.7) выразим из последних трех уравнений Δθрот, Δθв,вт и Δθк через Δθм и Δθс,ст:

; (2.8)

; (2.9)

. (2.10)

Подставив выражение (2.9) в первое уравнение системы (2.7) получим:

 Скачать реферат