Моделирование нагрева асинхронного двигателя
![]() – слагаемое, обуславливающее внутреннее тепловыделение.
– слагаемое, обуславливающее внутреннее тепловыделение.
Рассмотрим процесс нагрева тела с собственным тепловыделением мощностью P, с поверхности S которого происходит теплоотдача конвекцией и излучением при коэффициенте теплоотдачи α [1,3,5]. Для упрощения математического описания процесса вводятся следующие допущения:
2. Температура окружающей среды θс неизменна, то есть окружающая среда обладает неограниченной теплоемкостью.
3. Коэффициент теплоотдачи α между поверхностью машины и окружающей средой не зависит от места и длительности протекания процесса.
Уравнение теплового баланса составляется на том основании, что теплота, выделившаяся за элементарный промежуток времени dt, частично идет на изменение собственного теплосодержания тела и частично отводится в окружающую среду. В соответствии с этим уравнение теплового баланса имеет вид [1,3,5]:
где ΔP – выделяемые в данном объеме потери мощности;
θ – температура тела;
θс – температура окружающей среды;
c – удельная теплоемкость;
G – масса исследуемого объема тела;
α – коэффициент теплоотдачи с единицы площади поверхности;
F – площадь поверхности охлаждения.
В правой части уравнения (1.13) первое слагаемое обуславливает повышение температуры тела, а второе – обмен теплотой с окружающей средой.
После преобразования уравнение теплового баланса (1.13) принимает вид:
где C=с∙G – теплоемкость тела;
А=α∙F – коэффициент теплоотдачи тела.
1.2 Обзор методов теплового расчета и существующих моделей
В соответствии с разнообразием условий теплоотвода для теплового расчета электрических двигателей используются различные методы [4]:
1. Метод точного или приближенного аналитического решения уравнений для трех- или двухмерных температурных полей обычно применяется при значительной неравномерности поля. При этом зачастую требуются определенные упрощения геометрической формы и граничных условий в математической модели.
2. Численный метод сеток применяется в подобных случаях, но не требует значительных упрощений формы рассчитываемых областей пространства.
3. Метод одномерного температурного поля применяется для расчета распределения температуры по длине обмоток и других частей электрических машин. Основан на приведении трех- и двухмерных полей к одномерному путем упрощенного представления теплопередачи вдоль всех осей координат, кроме одной, с помощью дискретных параметров (тепловых сопротивлений).
4. Метод эквивалентных тепловых схем (ЭТС) получил наибольшее распространение ввиду простоты и достаточной точности расчета. Недостаток метода заключается в том, что он дает не полную картину температурного поля, а только некоторые средние значения температуры для отдельных элементов машины.
Данный метод основан на использовании тепловых сопротивлений [1], которые соединяются в тепловую сеть, имитирующую реальные пути передачи тепловых потоков в машине, и предполагает аналогию теплового потока с электрическим током, основанную на одинаковой форме основного закона теплопроводности (закон Фурье) [6]
и электрического тока (закон Ома)
где Fт – площадь сечения, перпендикулярного распространению теплоты;
λ – коэффициент теплопроводности;
Δθ – падение температуры на длине δ;
Rт – тепловое сопротивление данного участка на пути теплового потока;
k – удельная электрическая проводимость;
ΔU – разность потенциалов на длине проводника l с сечением Fпр;
Rэ – электрическое сопротивление.
Узлы тепловой схемы имитируют отдельные части двигателя. Если в какой-либо части двигателя присутствуют распределенные по объему источники теплоты, то при составлении эквивалентной тепловой схемы они заменяются сосредоточенным источником (источником теплового потока), помещенным в узел, имитирующий эту часть. Узлы с внутренним тепловыделением на схеме обозначаются кружками, узлы без тепловыделения – точками.
Для детального расчета значений температур используют подробные эквивалентные тепловые схемы. Так, например в [2] приводится тепловая схема закрытого обдуваемого двигателя (рисунок 1.2). Система уравнений для данной схемы в установившемся режиме:
где m – количество узлов эквивалентной тепловой схемы;
θв – температура воздуха снаружи машины;
Λki=1/Rki – тепловая проводимость соответствующего участка схемы;
Рi – потери в i-ом узле.
Отметим, что коэффициент теплоотдачи тела А в (1.14) и тепловые проводимости Λ в (1.17) имеют одинаковый физический смысл и размерность. Для расчета нестационарного режима используется та же тепловая схема, но каждый узел соединяется через емкость с внешним воздухом [4]. В этом случае электрическая емкость эквивалентна теплоемкости тела. Система уравнений для нестационарного режима:
где Сi – теплоемкость соответствующего узла схемы.
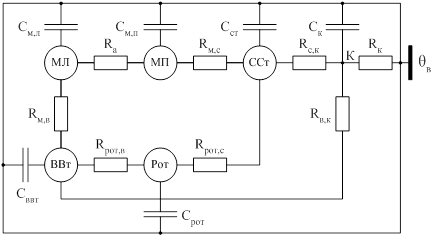
Однако авторы [4] замечают, что пользоваться подробными схемами с большим количеством узлов целесообразно лишь в редких случаях (например, при проектировании системы охлаждения машины). В практических расчетах конкретных машин удобнее использовать упрощенные эквивалентные тепловые схемы. Упрощения состоят в том, что симметричные узлы подробной схемы, находящиеся в приблизительно одинаковых условиях, объединяются (лобовые части обмотки, воздух внутри машины, подшипниковые щиты) и эквивалентными преобразованиями тепловая схема преобразовывается в схему с меньшим количеством узлов – источников тепловыделения. Объединение узлов, по сути, является заменой нескольких источников тепловыделения, сгруппированных по определенным признакам, в один. Так, в [4,9] предлагается приведенная эквивалентная тепловая схема закрытого обдуваемого двигателя (рисунок 1.3).
Рисунок 1.3 – Приведенная эквивалентная тепловая схема закрытого обдуваемого двигателя
Данная схема имеет шесть узлов: МЛ – лобовая часть обмотки, МП – пазовая часть обмотки, ВВт – воздух внутри машины, Рот – ротор, ССт – сталь сердечника статора, К – корпус двигателя (станина и подшипниковые щиты). Система уравнений нестационарного режима для схемы (см. рисунок 1.3) имеет вид [4,9]:
![]() , (1.13)
, (1.13)
![]() , (1.14)
, (1.14)
 (1.15)
(1.15)
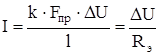 , (1.16)
, (1.16)
![]()
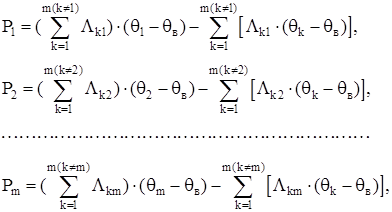 (1.17)
(1.17)
![]()
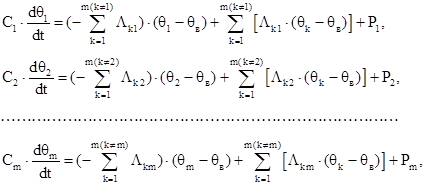 (1.18)
(1.18)
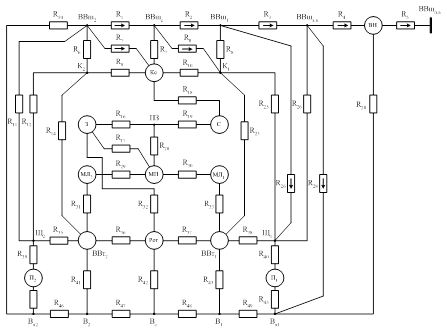
![]() Рисунок 1.2 – ЭТС закрытого обдуваемого двигателя, учитывающая неоднородность температуры корпуса
Рисунок 1.2 – ЭТС закрытого обдуваемого двигателя, учитывающая неоднородность температуры корпуса
Другие рефераты на тему «Физика и энергетика»:
Поиск рефератов
Последние рефераты раздела
