Моделирование нагрева асинхронного двигателя

Введение

Нестационарные тепловые процессы в электрических машинах имеют место при их эксплуатации. Ими сопровождаются режимы пуска, отключения, торможения, изменения нагрузки и частоты вращения машин. Большое значение процессы нестационарного нагрева имеют при перегрузках по току и напряжению, при частых и затяжных пусках двигателей, а так же при работе их в заторможенном состоянии

.

Особенностью нестационарных тепловых режимов, или тепловых переходных процессов, в электрических машинах является их инерционность, проявляющаяся в значительном отставании изменений температуры от электромеханических переходных процессов. Благодаря этому машины могут выдерживать в течение некоторого времени воздействие перегрузок, токов короткого замыкания и других ненормальных условий. Учет тепловой инерционности в расчетах нестационарного нагрева является обязательным условием достоверности результатов.

Повышенная температура электрических машин влияет на долговечность изоляции обмоток, на работу подшипников и др. Повышенная температура обмоток вызывает тепловое старение изоляции, приводящее к необратимому снижению электрической и механической прочности. Правило Монтзингера гласит, что повышение температуры на 8–100 С сокращает срок службы изоляции в два раза.

Основной целью данной работы является создание тепловой модели для выбора асинхронного двигателя по нагреву. Данная модель является упрощенным представлением процессов нагрева и охлаждения двигателя. Суть модели заключается в том, что, задавая характер изменения нагрузки во времени на входе, на выходе имеем кривую изменения температуры меди обмоток или стали статора.

1. Обзор литературы

1.1 Фундаментальные законы теплопередачи

В основе математической модели нагрева двигателя лежит основной закон теплопроводности [1,2,3,4,5], сформулированный Фурье в итоге анализа экспериментальных данных. Данный закон устанавливает количественную связь между тепловым потоком и разностью температур в двух точках тела: количество переданной теплоты пропорционально градиенту температуры, времени и площади сечения F, перпендикулярного к направлению распространения теплоты.

Если количество переданной теплоты отнести к единице времени, то сформулированная зависимость выразится следующим образом:

, (1.1)

где р – количество переданной теплоты, отнесенное к единице времени, то есть мощность;

λ – коэффициент теплопроводности;

F – площадь сечения, перпендикулярного к направлению распространения теплоты;

θ – температура точек тела.

Знак «минус» в (1.1) означает, что передача теплоты происходит в сторону, противоположную направлению градиента, то есть в сторону понижения температуры.

Коэффициент теплопроводности λ в уравнении (1.1) является физическим параметром и характеризует способность вещества проводить теплоту.

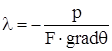, (1.2)

.

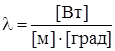Аналитическое решение, полученное путем непосредственного интегрирования уравнения (1.1), дает возможность вычислить температуру в любой точке системы. Однако решение уравнения в частных производных является довольно громоздким и слишком усложняет задачу. Поэтому на практике, для упрощения решения широко используется метод конечных разностей [3]. Сущность метода заключается в том, что в дифференциальном уравнении производные искомой функции заменяются приближенным соотношением между конечными разностями в отдельных узловых точках температурного поля. В результате такой замены получаем уравнение в конечных разностях, решение которого сводится к выполнению простых алгебраических операций:

, (1.3)

где δ – расстояние между исследуемыми точками;

Δθ – падение температуры на длине δ.

Для решения задач по определению температурного поля используют дифференциальное уравнение теплопроводности [1,2,3,4], которое выводится на основе закона сохранения энергии и закона Фурье. При выводе уравнения рассматривается нестационарное трехмерное температурное поле в однородном твердом теле, с распределенными по объему источниками теплоты. В пределах рассматриваемого тела берется элементарный объем dV=dx∙dy∙dz (рисунок 1.1), достаточно малый для того, чтобы считать физические параметры в нем постоянными, а потери – равномерно распределенными и пренебречь производными выше второго порядка от температуры θ по координатам.

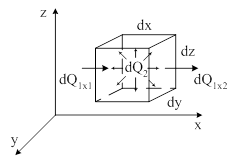
Рисунок 1.1 – Элементарный объем dV

Для элементарного объема dV составляется тепловой баланс за элементарный промежуток времени dt. Тепловой баланс является следствием закона сохранения энергии при допущении, что в энергетическом процессе не участвуют другие виды энергии, кроме тепловой:

, (1.4)

где dQ1 – тепловой поток, притекающий в объем dV за счет теплопроводности;

dQ2 – мощность источников теплоты, действующих внутри объема;

dQ – повышение внутренней энергии в объеме dV.

На рисунке 1.1 показаны только тепловые потоки, направленные вдоль оси x. Поток, притекающий слева, исходя из закона Фурье:

, (1.5)

тепловой поток, проходящий через противоположную грань (с учетом изменения производной ∂θ/∂x на интервале dx):

. (1.6)

Результирующий приток теплоты за единицу времени вдоль оси x:

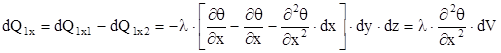. (1.7)

Аналогично для других координатных осей:

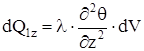; . (1.8)

Суммарный тепловой поток, притекающий в объем dV за счет теплопроводности:

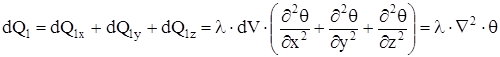. (1.9)

Мощность источников теплоты, действующих внутри объема:

, (1.10)

где р0 – мощность потерь в единице объема.

Изменение внутренней энергии в объеме dV:

, (1.11)

где с – удельная теплоемкость тела;

ρ – плотность материала тела.

Подставив (1.9), (1.10), (1.11) в (1.4) и проведя некоторые преобразования, получаем дифференциальное уравнение теплопроводности в частных производных:

. (1.12)

где – слагаемое, описывающее изменение теплосодержания тела;

– слагаемое, обуславливающее тепловой поток, притекающий в систему за счет теплопроводности;

 Скачать реферат