Эконометрическое моделирование финансового рынка

1) трендовой (Т), описывающей общее изменение со временем результативного признака;

2) сезонной (S), отражающей повторяемость данных через небольшой промежуток времени;

3) случайной (Е), отражающей влияние случайных факторов.

В большинстве случаев фактический уровень временного ряда можно представить как сумму или произведение трендовой, циклической и случайной компонент. Модель, в

которой временной ряд представлен как сумма перечисленных компонент, называется аддитивной моделью временного ряда. Модель, в которой временной ряд представлен как произведение перечисленных компонент, называется мультипликативной моделью временного ряда.

Основная задача эконометрического исследования отдельного временного ряда – выявление и придание количественного выражения каждой из перечисленных выше компонент с тем, чтобы использовать полученную информацию для прогнозирования будущих значений ряда или при построении моделей взаимосвязи двух или более временных рядов.

2.1 Моделирование тенденции временного ряда

Распространенным способом моделирования тенденции временного ряда является построение аналитической функции, характеризующей зависимость уровней ряда от времени, или тренда. Этот способ называют аналитическим выравниванием временного ряда.

Для построения трендов чаще всего применяются следующие функции: линейный тренд

(2.1)

Гипербола

(2.2)

экспоненциальный тренд

(или ) (2.3)

степенная функция

(2.4)

полиномы различных степеней:

(2.5)

Параметры каждого из перечисленных выше трендов можно определить обычным МНК, используя в качестве независимой переменной время

а в качестве зависимой переменной – фактические уровни временного ряда . Для нелинейных трендов предварительно проводят стандартную процедуру их линеаризации.

Наиболее простую экономическую интерпретацию имеет линейная функция : а – начальный уровень временного ряда в момент времени ; b – средний за период абсолютный прирост уровней ряда.

Параметры а и b находятся по формулам

(2.6)

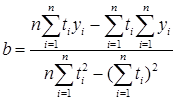(2.7)

Существует несколько способов определения типа тенденции. К числу наиболее распространенных способов относятся качественный анализ изучаемого процесса, построение и визуальный анализ графика зависимости уровней ряда от времени. В этих же целях можно использовать и коэффициенты автокорреляции уровней ряда. Тип тенденции можно определить путем сравнения коэффициентов автокорреляции первого порядка, рассчитанных по исходным и преобразованным уровням ряда. Если временной ряд имеет линейную тенденцию, то его соседние уровни и тесно коррелируют. В этом случае коэффициент автокорреляции первого порядка уровней исходного ряда должен быть высоким. Если временной ряд содержит нелинейную тенденцию, например, в форме экспоненты, то коэффициент автокорреляции первого порядка по логарифмам уровней исходного ряда будет выше, чем соответствующий коэффициент, рассчитанный по уровням ряда. Чем сильнее выражена нелинейная тенденция в изучаемом временном ряде, тем в большей степени будут различаться значения указанных коэффициентов.

Выбор наилучшего уравнения в случае, когда ряд содержит нелинейную тенденцию, можно осуществить путем перебора основных форм тренда, расчета по каждому уравнению скорректированного коэффициента детерминации и средней ошибки аппроксимации. Этот метод легко реализуется при компьютерной обработке данных.

2.2 Задачи анализа временных рядов. Первоначальная обработка временных рядов

Основные задачи анализа временных рядов. Базисная цель статистического анализа временного ряда заключается в том, чтобы по имеющейся траектории этого ряда:

1.определить, какие из неслучайных функций присутствуют в разложении (1), т.е. определить значения индикаторов ci;

2.построить «хорошие» оценки для тех неслучайных функций, которые присутствуют в разложении (1);

3.подобрать модель, адекватно описывающую поведение случайных остатков et, и статистически оценить параметры этой модели.

Успешное решение перечисленных задач, обусловленных базовой целью статистического анализа временного ряда, является основой для достижения конечных прикладных целей исследования и, в первую очередь, для решения задачи кратко- и среднесрочного прогноза значений временного ряда. Приведем кратко основные элементы эконометрического анализа временных рядов.

Временные ряды отражают тенденцию изменения параметров системы во времени, поэтому входным параметром х является момент времени.

Выходной параметр y называется уровнем ряда. В случае отсутствия ярко выраженных изменений в течение времени, общая тенденция сохраняется. Ряд можно описать уравнением вида

YT = F (t) + ET (2.8)

Где: F (t) – детерминированная функция времени.

ET – случайная величина

Во временных рядах проводится операция анализа и сглаживания тренда, который отражает влияние некоторых факторов. Для построения тренда применяется МНК-критерий.

Существуют моментальные и интервальные ряды. В моментальных рядах отражаются абсолютные величины, по состоянию на определенный момент времени, а в интервальных – относительные величины (показатель за год, месяц, и т.д.). Исследование данных при помощи рядов позволяет во многих случаях более четко представить детерминированную функцию. При этом рассчитываются базисные и цепные показатели (прирост, коэффициент роста, коэффициент роста, темп роста, темп прироста, и др.). Под базисными показателями понимают, показатели, которые соотносятся к начальному уровню ряда. Цепные показатели относятся к предыдущему уровню.

Прогноз явлений по временным рядам состоит из двух этапов:

- Прогноз детерминированной компоненты.

- Прогноз случайной компоненты.

Обе проблемы связаны с анализом результатов парных экспериментов. В отличие от аппроксимации и интерполяции анализ временных рядов включает в себя методы оценки случайных компонент. Поэтому прогнозирование при помощи временных рядов является более точным.

Исследование рядов имеет большое значение и для технических, и для экономических систем.

 Скачать реферат