Построение и анализ функции спроса на товар

В качестве второго фактора х2, влияющего на потребление, будем рассматривать размер семьи (данные приведены в таблице 6).

Таблица 7 Исходные данные по фактору Х2 - размер семьи

Как и в случае парной регрессии, мы выбираем значения коэффициентов регрессии так, чтобы обеспечить наилучшее соответствие наблюдениям. Получим систему из трех нормальных уравнений с тремя переменными:

(11)

Преобразуя эти уравнения можно получить формулы для расчета параметров а, b1 и b2.

Коэффициенты регрессии b1 и b2 - это показатели силы связи, характеризующие абсолютное (в натуральных единицах измерения) изменение результативного признака при изменении факторного признака на единицу своего измерения при фиксированном влиянии второго фактора.

Проверка значимости коэффициентов регрессии осуществляется, так же как и в парном регрессионном анализе с помощью t-критерия. Аналогично строятся и доверительные интервалы для каждого коэффициента регрессии.

В качестве показателей тесноты связи используются парные коэффициенты корреляции и частные коэффициенты корреляции.

Частные коэффициенты корреляции характеризуют тесноту связи между результатом и фактором при фиксированном влиянии других факторов, включенных в уравнение регрессии. Их можно определить через парные коэффициенты корреляции по следующим рабочим формулам:

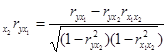(12)

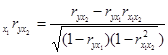(13)

где - коэффициент частной корреляции между результатом и фактором х1, при фиксированном воздействии фактора х2;

- коэффициент частной корреляции между результатом и фактором x2 при фиксированном воздействии фактора x1

,, -коэффициенты парной корреляции

Найдем коэффициент парной корреляции:

Тесноту связи между результатом и всеми факторами, включенными в уравнение регрессии, характеризует множественный коэффициент корреляции:

(14)

где s2фактор - факторная сумма квадратов, или объясненная моделью регрессия результата;

s2общ - общая сумма квадратов, или общая вариация результата;

s2остаточ = å (y - ŷ) 2 - остаточная сумма квадратов, или не объясненная моделью регрессии вариация результата.

Таблица 7

 Скачать реферат