Постановка и основные свойства транспортной задачи

Третья итерация. Первый этап.

Так как в матрице С3 нет отрицательных элементов, план Х2 – оптимальный.

Венгерский метод для транспортной задачи

Рассмотренная выше задача о назначениях представляет собой частный случай Т-задачи, когда . Поэтому венгерский метод, применимый для решения транспортной задачи специального вида, можно распространить на общий случай Т-задачи.

Пусть требуется решить Т-задачу следующего вида

минимизировать

при условиях

Алгоритм решения Т-задачи, основанный на венгерском методе, состоит из предварительного этапа и конечного числа однотипных итераций.

В результате предварительного этапа вычисляют матрицу , элементы которой удовлетворяют следующим условиям:

, (1.3.1)

. (1.3.2)

Если в условиях (1.3.1), (1.3.2) строгие равенства, то матрица Х0 является решением Т-задачи.

Матрицу, построенную в результате k-й итерации, обозначим . Обозначим также

. (1.3.3)

Величина называется суммарной невязкой для матрицы . Она характеризует близость к искомому плану Т-задачи. Итерации проводятся до тех пор, пока величина не станет равна нулю.

Описание алгоритма Венгерского метода

Предварительный этап. В каждом из столбцов матрицы транспортных издержек отыскивают минимальный элемент, который вычитают из всех элементов этого столбца. Получают матрицу С'. Далее в каждой строке матрицы С' выбирают минимальный элемент и вычитают его из всех элементов рассматриваемой строки. Приходят к матрице С0 (С0 ~ C), все элементы которой неотрицательны, причем в каждой строке и столбце С0 имеем по крайней мере, один нуль. Строят матрицу Х0 так, чтобы ее ненулевые элементы были расположены в позициях нулей матрицы С0.

Пусть - номер строки, в которой расположен k-й нуль j-го столбца матрицы С0. Тогда элементы первого столбца матрицы Х0 определяют по рекуррентной формуле

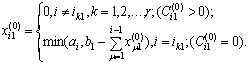(3.3.4)

 Скачать реферат