Понятие и классификация систем массового обслуживания

Для получения необходимых формул можно воспользоваться тем обстоятельством, что СМО на рисунок 5 является частным случаем системы рождения и гибели, представленной на рисунке 2, если в последней принять и

(21)

(22)

(23)

Выражения для финальных вероятностей состояний рассматриваемой СМО можно найти из (4) и (5) с учётом (21). В результате получим:

При р = 1 формулы (22), (23) принимают вид

При m = 0 (очереди нет) формулы (22), (23) переходят в формулы (14) и (15) для одноканальной СМО с отказами.

Поступившая в СМО заявка получает отказ в обслуживании, если СМО находится в состоянии Sm+1, т.е. вероятность отказа в обслуживании заявки равна:

Относительная пропускная способность СМО равна:

Абсолютная пропускная способность равна:

Среднее число заявок, стоящих в очереди Lоч, находится по формуле

и может быть записано в виде:

(24)

При формула (24) принимает вид:

– среднее число заявок, находящихся в СМО, находится по формуле(10)

и может быть записано в виде:

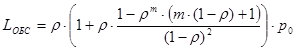(25)

При , из (25) получим:

Среднее время пребывания заявки в СМО и в очереди находится по формулам (12) и (13) соответственно.

5.4 Одноканальная система массового обслуживания с неограниченной очередью

Примером такой СМО может служить директор предприятия, вынужденный рано или поздно решать вопросы, относящиеся к его компетенции, или, например, очередь в булочной с одним кассиром. Граф такой СМО изображён на рисунке 6.

Рисунок 6 – Граф состояний одноканальной СМО с неограниченной очередью

Все характеристики такой СМО можно получить из формул предыдущего раздела, полагая в них . При этом необходимо различать два существенно разных случая: а) ; б) . В первом случае, как это видно из формул (22), (23), р0 = 0 и pk = 0 (при всех конечных значениях k). Это означает, что при очередь неограниченно возрастает, т.е. этот случай практического интереса не представляет.

Рассмотрим случай, когда . Формулы (22) и (23) при этом запишутся в виде:

Поскольку в СМО отсутствует ограничение на длину очереди, то любая заявка может быть обслужена, т.е. относительная пропускная способность равна:

Абсолютная пропускная способность равна:

Среднее число заявок в очереди получим из формулы (24) при :

Среднее число обслуживаемых заявок есть:

Среднее число заявок, находящихся в СМО:

Среднее время пребывания заявки в СМО и в очереди определяются формулами (12) и (13).

5.5 Многоканальная система массового обслуживания с ограниченной очередью

Пусть на вход СМО, имеющей каналов обслуживания, поступает пуассоновский поток заявок с интенсивностью . Интенсивность обслуживания заявки каждым каналом равна , а максимальное число мест в очереди равно .

Граф такой системы представлен на рисунке 7.

Рисунок 7 – Граф состояний многоканальной СМО с ограниченной очередью

– все каналы свободны, очереди нет;

– заняты l каналов (l = 1, n), очереди нет;

- заняты все n каналов, в очереди находится i заявок (i = 1, m).

Сравнение графов на рисунке 2 и рисунке 7 показывает, что последняя система является частным случаем системы рождения и гибели, если в ней сделать следующие замены (левые обозначения относятся к системе рождения и гибели):

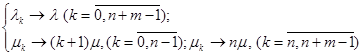
Выражения для финальных вероятностей легко найти из формул (4) и (5). В результате получим:

(26)

Образование очереди происходит, когда в момент поступления в СМО очередной заявки все каналы заняты, т.е. в системе находятся либо n, либо (n+1),…, либо (n + m – 1) заявок. Т.к. эти события несовместны, то вероятность образования очереди pоч равна сумме соответствующих вероятностей :

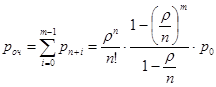(27)

Отказ в обслуживании заявки происходит, когда все m мест в очереди заняты, т.е.:

Относительная пропускная способность равна:

 Скачать реферат