Понятие и классификация систем массового обслуживания

, (30)

где – случайная величина, равномерно распределенная на интервале .

Т.е. выбрав очередное значение надо решить уравнение (30) и

найти очередное значение . Для доказательства рассмотрим функцию:

Имеем общие свойства плотности вероятности:

(31)

(32)

Из (31) и (32) следует, что , а производная .

Значит, функция монотонно возрастает от 0 до 1. И любая прямая , где , пересекает график функции в единственной точке, абсциссу которой мы и принимаем за . Таким образом, уравнение (30) всегда имеет одно и только одно решение.

Выберем теперь произвольный интервал , содержащийся внутри . Точкам этого интервала отвечают ординаты кривой, удовлетворяющие неравенству . Поэтому, если принадлежит интервалу , то

принадлежит интервалу , и наоборот. Значит: . Т.к. равномерно распределена в , то

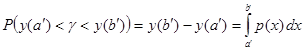, а это как раз и означает, что случайная величина , являющаяся корнем уравнения (30) имеет плотность вероятностей .

6.3 Случайная величина с экспоненциальным распределением

Простейшим потоком (или потоком Пуассона) называется такой поток заявок, когда промежуток времени между двумя последовательными заявками есть случайная величина, распределенная на интервале с плотностью

Вычислим математическое ожидание: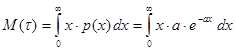

После интегрирования по частям, получим:

.

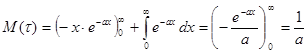Параметр есть интенсивность потока заявок.

Формулу для розыгрыша получим из уравнения (30), которое в данном случае запишется так: .

Вычислив интеграл, стоящий слева, получим соотношение . Отсюда, выражая , получим:

(33)

Т.к. величина распределена также как и , следовательно, формулу (33) можно записать в виде:

(34)

7 Исследование системы массового обслуживания

7.1 Проверка гипотезы о показательном распределении

Исследуемое мной предприятие представляет собой двухканальную систему массового обслуживания с ограниченной очередью. На вход поступает пуассоновский поток заявок с интенсивностью λ. Интенсивности обслуживания заявок каждым из каналов μ, а максимальное число мест в очереди m.

Начальные параметры:

Время обслуживания заявок имеет эмпирическое распределение, указанное ниже и имеет среднее значение .

Мной были проведены контрольные замеры времени обработки заявок, поступающих в данную СМО. Чтобы приступить к исследованию, необходимо установить по этим замерам закон распределения времени обработки заявок.

Таблица 6.1 – Группировка заявок по времени обработки

Выдвигается гипотеза о показательном распределении генеральной совокупности.

Для того чтобы, при уровне значимости проверить гипотезу о том, что непрерывная случайная величина распределена по показательному закону, надо:

1) Найти по заданному эмпирическому распределению выборочную среднюю . Для этого, каждый i – й интервал заменяем его серединой и составляем последовательность равноотстоящих вариант и соответствующих им частот.

 Скачать реферат