Понятие и классификация систем массового обслуживания

Т.к. , то нет оснований отвергнуть гипотезу о распределении X по показательному закону. Другими словами, данные наблюдений согласуются с этой гипотезой.

7.2 Расчет основных показателей системы массового обслуживания

Данная система представляет собой частный случай системы г

ибели и размножения.

Граф данной системы:

Рисунок 10 – Граф состояний исследуемой СМО

Поскольку все состояния являются сообщающимися и существенными, то существует предельное распределение вероятностей состояний. В стационарных условиях поток, входящий в данное состояние должен быть равен потоку, выходящему из данного состояния.

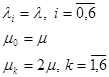(1)

Для состояния S0:

Следовательно:

Для состояния S1:

Следовательно:

С учетом того, что :

Аналогично получаем уравнения для остальных состояний системы. В результате получим систему уравнений:

Решение этой системы будет иметь вид:

; ; ; ; ;

; .

Или, с учетом (1):

; ; ; ; ; ;

.

Коэффициент загруженности СМО:

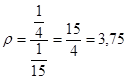
С учетом этого предельные вероятности перепишем в виде:

Наивероятнейшее состояние – оба канала СМО заняты и заняты все места в очереди.

Вероятность образования очереди:

Отказ в обслуживании заявки происходит, когда все m мест в очереди заняты, т.е.:

Относительная пропускная способность равна:

Вероятность того, что вновь поступившая заявка будет обслужена, равна 0,529

Абсолютная пропускная способность:

СМО обслуживает в среднем 0,13225 заявок в минуту.

Среднее число заявок, находящихся в очереди:

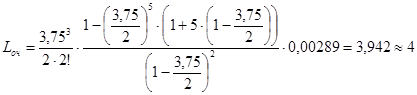
Среднее число заявок в очереди близко к максимальной длине очереди.

Среднее число заявок, обслуживаемых в СМО, может быть записано в виде:

В среднем все каналы СМО постоянно заняты.

Среднее число заявок, находящихся в СМО:

Для открытых СМО справедливы формулы Литтла:

Среднее время пребывания заявки с СМО:

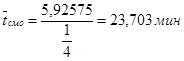
Среднее время пребывания заявки в очереди:

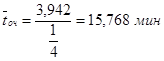
7.3 Выводы о работе исследуемой СМО

Наиболее вероятное состояние данной СМО – занятость всех каналов и мест в очереди. Приблизительно половина всех поступающих заявок покидают СМО необслуженными. Приблизительно 66,5% времени ожидания приходиться на ожидание в очереди. Оба канала постоянно заняты. Все это говорит о том, что в целом данная схема СМО неудовлетворительна.

Чтобы снизить загрузку каналов, сократить время ожидания в очереди и снизить вероятность отказа необходимо увеличить число каналов и ввести систему приоритетов для заявок. Число каналов целесообразно увеличить до 4. Также необходимо сменить дисциплину обслуживания с FIFO на систему с приоритетами. Все заявки теперь будут иметь принадлежность к одному из двух приоритетных классов. Заявки I класса имеют относительный приоритет по отношению к заявкам II класса. Для расчета основных показателей этой видоизмененной СМО целесообразно применить какой-либо из методов имитационного моделирования. Была написана программа на языке Visual Basic, реализующая метод Монте-Карло.

8 Исследование видоизмененной СМО

Пользователю при работе с программой необходимо задать основные параметры СМО, такие как интенсивности потоков, количество каналов, приоритетных классов, мест в очереди (если количество мест в очереди равно нулю, то СМО с отказами), а также временной интервал модуляции и количество испытаний. Программа преобразовывает сгенерированные случайные числа по формуле (34), таким образом, пользователь получает последовательность временных интервалов , распределенных показательно. Затем отбирается заявка с минимальным , и ставится в очередь, согласно ее приоритету. За это же время происходит перерасчет очереди и каналов. Затем эта операция повторяется до окончания времени модуляции, задаваемого изначально. В теле программы присутствуют счетчики, на основании показаний которых и формируются основные показатели СМО. Если для увеличения точности было задано несколько испытаний, то в качестве конечных результатов принимается оценка за серию опытов. Программа получилась достаточно универсальной, с ее помощью могут быть исследованы СМО с любым количеством приоритетных классов, либо вообще без приоритетов. Для проверки корректности работы алгоритма, в него были введены исходные данные классической СМО, исследуемой в разделе 7. Программа смоделировала результат близкий к тому, который был получен с помощью методов теории массового обслуживания (см. приложение Б). Погрешность, возникшая в ходе имитационного моделирования, может быть объяснена тем, что проведено недостаточное количество испытаний. Результаты, полученные с помощью программы для СМО с двумя приоритетными классами и увеличенным числом каналов, показывают целесообразность этих изменений (см. приложение В). Высший приоритет был присвоен более «быстрым» заявкам, что позволяет быстро обследовать короткие задания. Сокращается средняя длина очереди в системе, а соответственно минимизируется средство для организации очереди. В качестве основного недостатка данной организации можно выделить то, что «долгие» заявки находятся в очереди длительно время или вообще получают отказ. Введенные приоритеты могут быть переназначены после оценки полезности того или иного типа заявок для СМО.

 Скачать реферат