Электричество и магнетизм

5. Включить источ­ник питания постоянного тока. Плавно увеличивая ток в катушках Гельмгольца с помощью реостата, наблюдать изменение доменной структуры образца.

6. Определить ток, при котором доменная структура исчезает, и рассчитать напряженность магнитного поля по формуле:

Н= СI,

где С — постоянная катушки.

7. Уменьшая ток, зафиксиро­вать поле Нзар,

при котором возникают домены с противополож­ной намагниченностью. Уменьшить ток до нуля и наблюдать до­менную структуру в остаточном состоянии.

8. Поменять полярность источника, увеличивая обратный ток, перевести образец снова в насыщенное состояние.

9. Повторить процесс перемагничивания и соответст­вующие измерения несколько раз. Рассчитать по измеренным зна­чениям токов критические поля Hs, Нзар

Дополнительное задание

Наблюдение поведения микрокапельных агрегатов магнитной жидкости во внешнем магнитном поле

Магнитные жидкости - это высокоустойчивые коллоидные растворы твердых ферри- и ферромагнетиков в различных немагнитных средах (керосине, воде, толуоле, минеральных и кремнийорганических маслах). Магнитные жидкости обладают уникальным свойством сохранять однородность в течение многих лет и иметь в жидком состоянии высокие магнитную восприимчивость и намагниченность насыщения, что позволяет широко использовать их в технике и современных технологиях. Основным средством управления магнитными жидкостями является магнитное поле. При некоторых условиях в магнитной жидкости образуются спонтанно намагниченные микрокапельные агрегаты. Во внешнем магнитном поле микрокапельные агрегаты вытягиваются вдоль вектора напряженности магнитного поля и образуют цепочки. Микрокапельные агрегаты обладают высокой магнитной проницаемостью и низким значением коэффициента межфазного натяжения на границе с менее концентрированной магнитной жидкостью. Возможность управления деформацией микрокапельных агрегатов слабым внешним магнитным полем позволяет широко использовать такие жидкости (магнитная дефектоскопия, магнитография).

1. Нанести капельку магнитной жидкости с микрокапельными агрегатами на предметное стекло и накрыть ее покровным стеклом.

2. Поместить образец на предметный столик микроскопа.

3. Микроскоп с образцом поместить в область однородного магнитного поля катушек Гельмгольца.

4. Подать напряжение на катушки от источника постоянного тока.

5. Изменяя магнитное поле катушек наблюдать поведение микрокапельных агрегатов.

6. Пронаблюдать за поведением агрегатов при повороте образца в магнитном поле.

7. Сделать вывод и зарисовать полученную картину.

Контрольные вопросы:

1. Магнитные свойства вещества Теория магнетизма.

2. Теория ферромагнетизма.

3. Замкнутая и открытая доменные структуры.

4. Общие представления о магнитных жидкостях.

5. Применение магнитных жидкостей.

Литература, рекомендуемая к лабораторной работе:

1. Матвеев А.Н. Электричество и магнетизм.- М.: Высшая школа, 1983.

2. Савельев И.В. Курс общей физики. Т.2, Т. 3. – М.: Наука, 1977.

3. Калашников С.Г. Электричество. – М.: Наука, 1977.

4. Телеснин Р.В., Яковлев В.Ф. Курс физики. Электричество.-М.: Просвещение, 1970.

5. Сивухин Д.В. Общий курс физики. Т.3. Электричество.- М.: Физматлит МФТИ, 2002.

6. Зильберман Г.Е. Электричество и магнетизм. – М.: Наука, 1970.

7. Парсел Э. Курс физики Т.2 Электричество и магнетизм – М.: Наука, 1971.

8. Буравихин В.А., Шелковников В.Н., Карабанова В.П. Практикум по магнетизму. – М.: Высшая школа, 1979.

9. Руководство к лабораторным занятиям по физике. Под редакцией Л.Л. Гольдина, - М.: Наука, 1983.

ЛАБОРАТОРНАЯ РАБОТА №13

ИЗУЧЕНИЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА

Цель работы:

Ознакомление с одним из методов измерения индуктивности катушки, электроёмкости конденсатора и изучение закона Ома для цепей переменного тока.

Идея эксперимента

Проверка закона Ома сводится к сравнению сопротивления участ­ка цепи,

содержащего последовательно соединенные катушку индук­тивности и

конденсатор, вычисленного по показаниям амперметра и вольтметра (Zизм=U/I) с рассчитанным по формуле

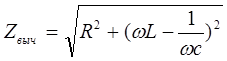
где R , L и С - величины, вычисленные при выполнении пре­дыдущих заданий.

Теоретическая часть

Переменный ток

Переменным током называется ток, гармонически изменяющийся во времени

I=I0sin(ωt+φ),

где I0 - амплитудное значение тока, φ - начальная фаза и ω -циклическая частота. При прохождении переменного тока по провод­нику в нем возникает э.д.с. самоиндукции, пропорциональная изме­нению силы тока в единицу времени

Коэффициент пропорциональности L называется индуктивностью про­водника и зависит от формы и размеров проводника, а также от магнитных свойств окружающей среды. За единицу индуктивности в СИ принимается I Гн (генри) - это индуктивность такого проводника, в котором изменение силы тока на I А за 1 секунду создаёт э.д.с. самоиндукции в I В. У линейных проводников индуктивность мала. Большой индуктивностью обладают катушки индуктивности, состоящие из большого числа витков. Сопротивление проволоки, которой намотана катушка, постоянному току называется активным (омическим) сопротивлением. При наличии этого сопротивления в цепи выделяется энергия.

Если к концам проводника с активным сопротивлением R при­ложено переменное напряжение, величина которого в каждый момент времени t определяется уравнением:

U=U0 cos ωt , (1)

где Uо - амплитудное значение напряже­ния, то в проводнике возникает переменный электрический ток, сила которого в тот же момент времени определяется по закону Ома

(2)

Ток и напряжение в этом случае изменяются синфазно, сдвиг фаз ме­жду ними равен нулю.

Индуктивность и ёмкость в цепи переменного тока

Если на участке цепи имеется катушка индуктивности L , активным сопротивле­нием которой можно пренебречь, то ток

, (3)

где I0=U0/ωL. Роль сопротивления в этом случае играет вели­чина XL=ωL, которую называют индуктивным сопротивлением. Ток через индуктивность отстаёт по фазе от приложенного напряжения на π/2.

Если участок цепи состоит из соеди­нённых последовательно активного сопро­тивления R и индуктивности L , то ток

, (4)

где (5)

φ-сдвиг фаз между током и напряжением, и tg φ= ωL/R. .Величина

(6)

носит название полного сопротивления, так как она играет в формуле (5) ту же роль, что и активное сопротивление в законе Ома.

 Скачать реферат