Электричество и магнетизм

При абсолютном нуле энергия кристалла должна быть минимальной. Поэтому валентные электроны заполняют попарно нижние уровни разрешенной зоны, возникшей из того уровня, на котором находятся валентные электроны в основном состоянии атома (валентная зона). Более высокие разрешенные зоны будут от электронов свободны. В зависимости от степени заполнения валентной зоны электронами и ширины запретной з

оны возможны три случая, изображенные на рисунке 1. В случае а) электроны заполняют валентную зону не полностью, поэтому достаточно сообщить электронам, находящимся на верхних уровнях, совсем небольшую энергию (~ 10 -23÷10-22 эВ) для того, чтобы перевести их на более высокие уровни. Энергия теплового движения составляет при 1К величину порядка 10-4эВ. Следовательно, при температурах отличных от 0 К часть электронов переводится на более высокие уровни. Дополнительная энергия, вызванная действием на электрон электрического поля, также оказывается достаточной для перевода на более высокие уровни. Поэтому электроны могут ускоряться электрическим полем и приобретать дополнительную скорость в направлении, противоположном направлению поля. Таким образом, кристалл с подобной схемой энергетических уровней будет представлять собой металл. Частичное заполнение валентной зоны (в случае металла ее также называют зоной проводимости) может произойти, если на последнем занятом уровне в атоме находится только один электрон; или имеет место перекрывание зон. В первом случае N электронов проводимости заполняют попарно только половину уровней валентной зоны. Во втором случае число уровней в зоне проводимости будет больше N, так, что даже если количество электронов проводимости равно 2N, они не смогут занять все уровни зоны.

В случаях б) и в) уровни валентной зоны полностью заняты электронами – зона заполнена. Для того чтобы увеличить энергию электрона, необходимо сообщить ему количество энергии, не меньшее, чем ширина запретной зоны ΔW. Электрическое поле сообщить электрону такую энергию не в состоянии. При этих условиях электрические свойства кристалла определяются шириной запретной зоны ΔW. Если ΔW невелико (порядка нескольких десятых эВ) энергия теплового движения оказывается достаточной для того, чтобы перевести часть электронов в верхнюю свободную зону. Эти электроны будут находиться в условиях, аналогичных тем, в которых находятся валентные электроны в металле. Свободная зона окажется зоной проводимости. Одновременно станет возможным переход электронов валентной зоны на ее освободившиеся верхние уровни. Такое вещество называется электронным полупроводником.

Если ширина запрещенной зоны ΔW велика (порядка нескольких эВ), тепловое движение не сможет забросить в свободную зону заметное число электронов. В этом случае кристалл оказывается изолятором.

Таким образом, квантовая теория объясняет с единой точки зрения существование хороших проводников (металлов), полупроводников и изоляторов.

Итак, полупроводниками являются кристаллические вещества, у которых валентная зона полностью заполнена электронами, а ширина запрещённой зоны невелика (не более 1 эВ). Полупроводники обязаны своим названием тому обстоятельству, что по величине электропроводности они занимают промежуточное положение между металлами и диэлектриками. Однако, характерным для них является не величина проводимости, а то, что их проводимость растёт с повышением температуры (у металлов она уменьшается).

Электрическое поле не может перебросить электроны из валентной зоны в зону проводимости. Поэтому полупроводники ведут себя при абсолютном нуле как диэлектрики. При температурах, отличных от 0 К, часть электронов из валентной зоны переходит в зону проводимости, в результате чего в полупроводнике возникают свободные носители зарядов. С повышением температуры число таких носителей растёт и, следовательно, увеличивается электропроводность полупроводника, а значит, уменьшается сопротивление. Зависимость сопротивления полупроводников от абсолютной температуры в опреде­лённых температурных интервалах описывается формулой

, (4)

где А - константа, k - постоянная Больцмана, ΔЕ - энергия активации. Под энергией активации понимается энергия, которую нужно затратить, чтобы перевести электрон из валентной зоны в зону проводимости. Логарифмирование уравнения (4) даёт

. (5)

График зависимости ln(R)=f(1/T) представляет собой прямую, уг­ловой коэффициент которой равен ΔЕ/К. Построив график зависимости (5), этот угловой коэффициент можно определить по формуле

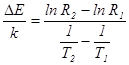(6)

для любых двух точек, лежащих на прямой, а затем найти энергию активации ΔЕ.

Экспериментальная установка

Исследуемые проводник и полупроводник помещаются в термостат, заполненный непроводящей жидкостью. В нижней части термостата помещен нагреватель. Температура измеряется термометром. Сопротивления проводника и полупроводника изме­ряются одновременно с помощью измерителя иммитанса (рис.2). Для проведения измерения достаточно подключить проводник (полупроводник) к зажимам и установить нужный режим измерения. Нажатием кнопки «Параметр» установить прибор в режим измерения RG. Так как истинная температура проводника и полупроводника может нес­колько отличаться от показаний термометра в условиях нагревания и охлаждения, то сопротивление следует измерять дважды: при нагревании, а затем при охлаждении, и вычислять среднее значение.

Проведение эксперимента

1. Исследуемые проводник и полупроводник подключить к клеммам измерителей иммитанса в качестве неизвестного сопротивления;

2. Измерить их сопротивления при комнатной температуре;

3. Включить нагреватель и измерять сопротивления Rпов. через каждые 4-5° С при повышении температуры до 50-60° С;

4. Выключить нагреватель и произвести измерения сопротивлений Rпон. проводника и полупроводника при их охлаждении до комнатной температуры;

5. Результаты измерений занести в таблицы 1 и 2;

6. Определить среднее значение сопротивлений, измеренных при повышении и понижении температуры;

7. Построить график зависимости проводника R= f(T), откладывая по горизонтальной оси температуру, а по вертикальной – сопротивление;

8. Из графика определить R0 и α следующим образом: продлить полученную прямую до пересечения с осью R. Точка пересечения даст значение R0 . Значение коэффициента α вычислить по формуле (3), воспользовавшись данными графика.

9. Построить график зависимости lnR=f(1/T), откладывая зна­чения 1/Т по горизонтальной оси, a In R - по вертикальной.

10. Пользуясь формулой (6), определить угловой коэффициент, а затем и энергию активации полупроводника Е Выразить энергию активации в электрон-вольтах.

Таблица I

 Скачать реферат