Электричество и магнетизм

29. Парсел Э. Курс физики Т.2 Электричество и магнетизм – М.: Наука, 1971.

30. Физический пракимкум. Электричество. Под редакцией В.И. Ивероновой. – М.: Наука, 1968.

31. Кортнев А.В., Рублев Ю.В., Куценко А.Н Практикум по физике. – М.: Высшая школа, 1965.

32. Руководство к лабораторным занятиям по физике. Под редакцией Л.Л. Гольдина, - М.: Наука, 1983.

ЛАБОРАТОРНАЯ

РАБОТА № 15

ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ

Цель работы:

Получить и наблюдать с помощью осциллографа за­тухающие электромагнитные колебания, определить логарифмический декремент затухания и его зависимость от параметров колебатель­ного контура.

Идея эксперимента

Для возбуждения колебаний в контуре используется метод электрического удара: в цепь колебательного контура на конденса­тор подаётся короткий электрический импульс, он заряжает конден­сатор, и в цепи возникают затухающие колебания. В качестве источ­ника электрических импульсов используется пилообразное напряже­ние генератора развёртки осциллографа. Для получения на экране осциллографа кривой U(t), можно воспользоваться схемой на рис. 1. На пластины осциллографа подается сигнал U пропорциональный току в контуре. Реле К 1-2 попеременно подключает конденсатор то к источнику импульсов, то к колебательному контуру, поэтому на экране осциллографа видна устойчивая картина (рис. 2). При этом условие синхронизации двух процессов - развёртки и затухающего колебания - выполняется автоматически, так как час­тота следования импульсов связана с частотой развёртки.

Теоретическая часть

Реальный колебательный контур

Замкнутая цепь, состоящая из катушки индуктивности и ёмкости, образует колебательный контур. Реальный колебательный контур обладает сопротивлением. Колебания в контуре можно вызвать, сообщив обкладкам конденсатора некоторый начальный заряд, либо возбудив в индуктивности ток, например, путём выключения внешне­го магнитного поля, пронизывающего витки катушки.

Рассмотрим цепь, изображённую на рис.1. Если зарядить кон­денсатор от источника тока ε (ключ К в положении I), а за­тем замкнуть конденсатор на

электрического поля будет убывать, но зато возникает всё возрастающая энергия маг­нитного поля, обусловленного током, текущим через индуктивность. В катушке возникает э.д.с. самоиндукции, направленная так, чтобы поддержать ток. Поэтому в момент, когда напряжение на конденса­торе обратится в нуль, ток достигнет наибольшего значения.

Далее ток течёт за счёт э.д.с. самоиндукции и перезаряжает конденсатор, но уже до меньшего напряжения, так как часть энер­гии выделяется в виде джоулева тепла на сопротивлении R Затем те же процессы протекают в обратном направлении, после чего сис­тема приходит в исходное состояние.

Таким образом, в колебательном контуре периодически изменяют­ся (колеблются) заряд на обкладках конденсатора, напряжение на конденсаторе и сила тока, текущего через индуктивность. Колеба­ния сопровождаются взаимными превращениями энергии электрическо­го и магнитного полей.

На основании закона Ома

. , (1)

где U - напряжение на конденсаторе, εi - э.д.с. самоиндукции.

; , (2)

так как q=UC. Знак "минус" указывает, что положительным считается то направление тока, которое соответствует убыли заря­да на конденсаторе. Из формул (2) находим:

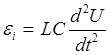. (3)

Из соотношений (I), (2) и (3) получается дифференциальное урав­нение затухающих колебаний:

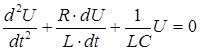. (4)

Введём обозначения: ω0 = (1/LC)1/2 - циклическая частота соб­ственных колебаний контура без затухания, β= R/2L коэффициент затухания. Тогда уравнение (4) можно записать в виде:

. (5)

Решением этого уравнения будет выражение:

(б)

где (7)

циклическая частота свободных колебаний контура. Из уравнения (6) следует, что напряжение на конденсаторе со временем изменяется по гармоническому закону. Амплитуда колебаний убывает со временем по экспоненциальному закону. Вид затухающих колебаний представлен на рис. 2. Период колебаний выражается формулой:

. (8)

Если R достаточно мало по сравнению с L , то членом R2/4L2 можно пренебречь, и (8) переходит в формулу Томсона:

. (9)

Для характеристики затухания колебаний служит логарифмический декремент затухания – натуральный логарифм отношения двух амплитуд, отстоящих друг от друга по времени на один период.

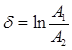, (10)

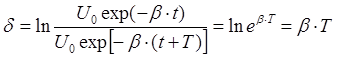При сопротивлении , когда выражение (8) обращается в бесконечность, колебания в контуре не возникают, а процесс будет называться апериодическим.

Экспериментальная установка

Схема экспериментальной установки изображена на рис. 3. Емкость С,

индуктивность L и сопротивление R образуют колебательный контур. Колебания в контуре наблюдаются с помощью осциллографа. Для возбуждения колебаний служит генератор импульсов, присоединенный к контуру через конденсатор C1.

Конденсатор контура получает некоторый начальный заряд. В промежутках между импульсами в контуре совершаются свободные колебания, описываемые уравнением (5). Затухание колебаний определяется потерями энергии в катушке индуктивности L и сопротивлении R

Проведение эксперимента.

Изучение зависимости логарифмического декремента затухания от ёмкости

1. Собрать цепь по схеме (рис. 3), включив конденсатор электро­ёмкостью С= 13600 пФ.

 Скачать реферат