Электричество и магнетизм

Отсюда видно, что lnI является линейной функцией времени t с угловым коэффициентом 1/τ. (рис.1). Угловой коэффициент прямой есть скорость изменения функции по данному параметру и, следовательно, может

.

быть рассчитан как тангенс угла наклона прямой lnI(t) к оси абсцисс. Т.е.

=105 height=49 src="images/referats/9136/image032.png">.

Таким образом, время релаксации цепи τ можно определить, построив график зависимости lnI(t) по экспериментальным результатам. Величина сопротивления R рассчитывается из соотношения RI0=ε. После определения R и τ, можно найти C из соотношения:

С=τ/R. (1)

Теоретическая часть

В области электрических явлений большой интерес представляют переходные процессы, которые имеют место при разрядке и зарядке конденсаторов. Эти процессы используются во времязадающих узлах электронных схем, применяющихся в электронно-вычислительной технике (одно- и мультивибраторы), узлах развертки осциллографов, дисплеев, генераторов электрических колебаний звуковой и радиочастоты.

Задачи о зарядке и разрядке конденсатора, строго говоря, выходят за рамки учения о постоянных токах. Приводимые ниже решения получаются в предположении, что мгновенное значение тока одно и то же во всех поперечных сечениях провода, соединяющего обкладки конденсатора, а мгновенное электрическое поле такое же, как в электростатике при тех же зарядах на обкладках конденсатора. Токи и поля, удовлетворяющие этому условию, называются квазистационарными.

Если обкладки заряженного конденсатора (рис 2) соединить проводом, то по проводу потечет ток Пусть I, Q, и U - мгновенные значения тока, заряда на конденсаторе и напряжение на его обкладках Считая ток в проводе положительным, когда он течет от положительной обкладки к отрицательной, можно написать:

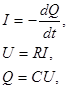
где С - емкость конденсатора, R - сопротивление провода. Исключая I и U, можно получить: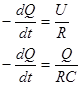

После интегрирования этого уравнения получается соотношение

(1)

где Q0 - начальное значение заряда конденсатора (Q=Qo при t=0 ), а т - время релаксации. Дифференцируя (1) по времени t, можно найти закон изменения разрядного тока во времени:

или

, (2)

где Iо = Q /τ - начальное значение тока, т.е. ток при t = 0.

Аналогично решается задача о зарядке конденсатора. Пусть в цепь конденсатора с емкостью С включен какой-нибудь источник тока с постоянной электродвижущей силой ε (рис.3).

Ток, идущий от источника, заряжает конденсатор. Электрические заряды, появляющиеся на обкладках конденсатора, препятствуют прохождению тока и уменьшают его. Можно записать, что

,

где R - полное сопротивление провода, соединяющего обкладки конденсатора и внутреннее сопротивление источника. Исключая снова I и U, получим уравнение

или

Это неоднородное уравнение сведется к однородному, если его записать в виде , так как εС = const. Решение этого уравнения получится в виде

Значение постоянной интегрирования А найдется из условия, что в начальный момент времени конденсатор не заряжен, т. е. в этот момент времени Q = 0. Это дает А = -ε С, следовательно,

При t → ∞ заряд конденсатора стремится к предельному значению

Q =ε С. Для тока можно получить или (3)

где I0 = ε/R - максимальный ток в начальный момент времени. В дальнейшем он убывает по экспоненциальному закону.

Экспериментальная установка

Для экспериментального определения емкости конденсаторов в данной работе используется установка, принципиальная схема которой приведена на рис.4. Переключатель П служит для обеспечения разных режимов работы схемы. Положение 1-1 служит для измерения начального тока I0, положение 2-2 соответствует зарядке конденсатора, а 3-3 - его разрядке. С помощью переключателей П1 и П2 можно подключать различные сопротивления и конденсаторы

Проведение эксперимента

1. Экспериментальную установку подключить к самопишущему устройству.

2. Включить самопищущее устройство.

3. Включить источник питания ВУП-2, убедившись, что ручка регулировки напряжения источника на нуле.

4. Установить тумблеры переключателя рода работ в положение Io , R2, С2.

5. Вращая ручку регулировки напряжения установить ток в цепи 90 мкА, напряжение при этом 185 В.

6. Опустить перо на диаграммную ленту нажатием кнопки UP/DOWN на самопишущем устройстве и отметить ток 1о.

7. Привести диаграммную ленту в движение кнопкой START/STOP, одновременно поставив переключатель рода работ в положение ЗАРЯД.

8. Наблюдать за изменением силы тока, пока ток не станет равным нулю, подписать полученную диаграмму.

9. Остановить движение ленты нажатием кнопки START/STOP.

10.Вернуть ленту в начальное положение нажатием кнопки FEED

11.Выполнить пункты 3-10 для R 1C2, R2C1, R1 C1.

12.Срезать диаграммную ленту.

13.Построить логарифмические кривые ln I=f(t) для полученных диаграмм (см. рис.1)

14.По графикам определить τ - время релаксации.

15.Заполнить таблицу

16.Определить по формуле 1 C1 и С2.

Таблица 1.

 Скачать реферат