Программирование на сетях

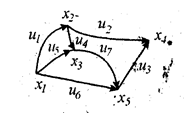
Рис.1.2

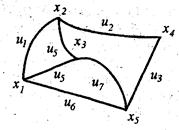
Рис.1.3

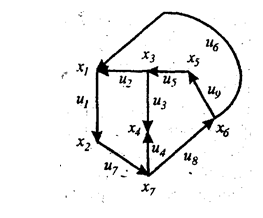
Для ориентированных и неориентированных графов можно сформировать матрицу смежности вершин. Пусть орграф G содержит n вершин. Его матрица смежности представляет собой квадратную матрицу n-го порядка. Строки и столбцы этой матрицы соответствуют вершинам орграфа G. Элементы uBij Bесть число дуг, выходящих из i-й вершины и входящий в j-ю. В орграфе, не содержащем параллельных дуг, элементами матрицы будут 1 и 0. На рис. 1.4. представлен орграф и его матрица смежности вершин. Как видно из рис. 1.5, у неориентированного графа матрица смежности вершин будет симметрической. По матрице смежности вершин определяется степень вершины, т.е. число дуг, пересекающихся в этой вершине. Число входящих в i-ю вершину дуг равно сумме элементов i- го столбца; число дуг, исходящих из данной вершины, равно сумме элементов i-й строки.

 Скачать реферат