Парная и множественная регрессия и корреляция

Вывод остатка

2. Нелинейные модели регрессии и их линеаризация

Цель работы: ознакомиться с методикой расчета показателей парной нелинейной регрессии и корреляции, овладеть приемами построения нелинейных регрессионных моделей с помощью MS Exсel.

РЕШЕНИЕ:

2.1.1 Регрессия в виде степенной функции имеет вид:

.

Для оценки параметров модели линеаризую (привожу к линейному виду) модель путем логарифмирования: .

Обозначаю lny =Y, lna =A, lnx =X.

Тогда получаю: Y=A+bX.

Для расчетов составляю с помощью MS Excel вспомогательную таблицу, в которой рассчитаю натуральные логарифмы с помощью математической функции LN (рисунок 7).

Рисунок 7 Расчет натуральных логарифмов

Далее с помощью инструмента Регрессия рассчитываю параметры уравнения (рисунки 8, 9).

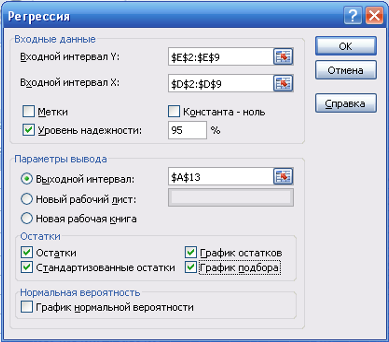
Рисунок 8 Диалоговое окно Регрессия

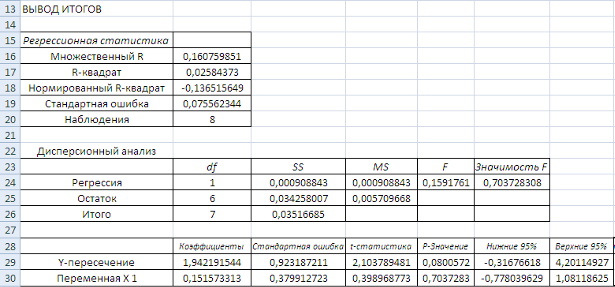
Рисунок 9 Результаты расчета параметров степенной функции

Таким образом, уравнение регрессии имеет вид:

.

Выполнив потенцирование, получим:

.

Параметр b=0,151 означает коэффициент эластичности, который показывает, что с ростом величины среднедушевых доходов населения на 1% общий коэффициент рождаемости увеличится в среднем на 0,151%.

2.1.2 Регрессия в виде экспоненты имеет вид:

. (13)

Для оценки ее параметров необходимо привести уравнение к линейному виду:

.

Для расчета параметров экспоненциальной прямой можно воспользоваться статистической функцией ЛГРФПРИБЛ MS Excel. Результаты вычислений представлены на рисунке 10.

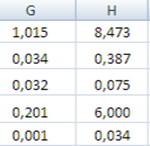
Рисунок 10 Результаты вычислений параметров экспоненциальной функции

Таким образом, уравнение регрессии в виде экспоненты имеет вид:

.

2.1.3 Регрессия в виде равносторонней гиперболы имеет вид:

,

чтобы оценить параметры a и b, привожу модель к линейному виду, заменив

.

Тогда

.

Результаты замены представлены на рисунке 11.

Рисунок 11 Вспомогательная таблица для расчета параметров гиперболы

Далее с помощью инструмента Регрессия рассчитываю параметры уравнения. Результаты расчета представлены на рисунке 12.

Рисунок 12 Результаты вычислений параметров гиперболической функции

Выберем наилучшую модель, для чего объединим результаты построения парных регрессий в одной таблице 3.

Все уравнения регрессии достаточно хорошо описывают исходные данные.

Таблица 3 Результаты корреляционно-регрессионного анализа

 Скачать реферат