Парная и множественная регрессия и корреляция

.

Параметры уравнения можно определить и по следующим формулам:

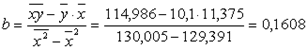
= 10,1 – 0,1608. 11,375= 8,2709

Величина коэффициента регрессии b = 0,1607 означает, что с ростом среднедушевых доходов на

1 тыс. руб. общий коэффициент рождаемости увеличится в среднем на 0,1607 раз.

1.1.2 Средний коэффициент эластичности для линейной регрессии находится по формуле:

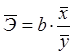
0,181

При увеличении величины среднедушевого дохода на 1%, общий коэффициент рождаемости в среднем увеличится на 0,181%.

1.1.3 Линейный коэффициент парной корреляции (r) определяется по формуле:

,

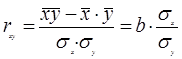где средние квадратические отклонения:

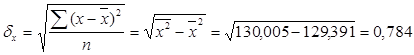
тогда , значит связь между среднедушевым доходом и рождаемостью очень слабая.

1.1.4 Определим коэффициент детерминации:

Таким образом, вариация величины рождаемости на 3,6% зависит от вариации уровня среднедушевых доходов населения, а на остальные (100%-3,6%) 96,4% − от вариации факторов, не включенных в модель.

Подставляя в уравнение регрессии фактические значения x, определим теоретические (расчетные) значения (таблица 1) и найдем величину средней ошибки аппроксимации ():

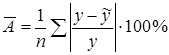==0,425

Так как допустимый предел значений не более 8-10%, качество модели по данному показателю удовлетворительное. Однако средняя ошибка аппроксимации не является главным критерием оценки значимости модели.

С помощью F−критерия Фишера оценим статистическую надежность результатов регрессионного моделирования:

Fфакт==.

Fтабл = 5,99 при .

Так как Fфакт < Fтабл, уравнение регрессии не значимо, статистически не надежно.

1.2 Решение задачи с помощью MS Excel

1.2.1 Параметры линейной регрессии

можно определить с помощью встроенной статистической функции ЛИНЕЙН MS Excel. Порядок вычисления следующий:

1) ввожу исходные данные (рисунок 1).

2) выделяю область пустых ячеек 5´2 (5 строк, 2 столбца) с целью вывода результатов регрессионной статистики или область 1´2 – для получения только оценок коэффициентов регрессии;

3) активизирую Мастер функций любым из способов:

а) в главном меню выбираю Вставка / Функция;

б) на панели инструментов Стандартная щелкаю по кнопке Вставка функции;

Рисунок 1 Ввод данных для корреляционно-регрессионного анализа

4) в окне «Категория» выбераю Статистические, в окне «Функция» – ЛИНЕЙН. Щелкаю по кнопке ОК (рисунок 2);

Рисунок 2 Диалоговое окно Мастер функций

5) заполняю аргументы функции (рисунок 3):

Рисунок 3 Диалоговое окно Аргументы функции

Щелкаю по кнопке ОК;

6) в левой верхней ячейке выделенной области появился первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажимаю на клавишу <F2>, а затем – на комбинацию клавиш <CTRL> + <SHIFT> + <ENTER>.

Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:

Результаты вычислений функции ЛИНЕЙН представлены на рисунке 4.

Рисунок 4 Результаты вычислений функции ЛИНЕЙН

1.2.2 С помощью инструмента анализа данных Регрессия, помимо результатов регрессионной статистики, дисперсионного анализа и доверительных интервалов, можно получить остатки и графики подбора линии регрессии, остатков и нормальной вероятности. Порядок действий следующий:

1) проверяю доступ к пакету анализа. В главном меню последовательно выбераю Сервис / Настройки. Устанавливаю флажок Пакет анализа;

2) в главном меню выбираю Сервис / Анализ данных / Регрессия. Щелкаю по кнопке ОК;

3) после вызова режима Регрессия на экране появляется диалоговое окно (рисунок 5), в котором задаются следующие параметры:

Рисунок 5 Диалоговое окно режима Регрессия

Результаты регрессионного анализа для исходных данных представлены на рисунке 6.

Вывод итогов

Дисперсионный анализ

 Скачать реферат