Оценка инвестиционных процессов

Всего кредитор выплатит 141250 рублей

Схема 4

Погашение кредита равными годовыми выплатами

При данной форме расчетов в конце каждого года выплачивается одинаковая сумма R.

,

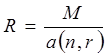где a(n,r) – коэффициент приведения ренты.

Эти платежи можно рассматривать как ежегодную ренту заемщика (кредитора). В этом случае,

сумма M представляет собой современную выплату ренты, а R - ежегодный рентный платеж.

a(10;7,5) = 6,864

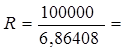14568,59 (руб)

Ежегодные выплаты – 14568,59 рублей.

Итого за 10 лет: 145685,93 рублей.

Задание №3. Балансовые модели. Модель Леонтьева

Для системы трех отраслей задана матрица прямых затрат А и вектор конечной продукции Y в стоимостном выражении.

Определить:

1. Величину валовой продукции для каждой отрасли и заполнить балансовую таблицу.

2. За счет роста экспорта производство конечной продукции третьей отрасли возросло на λ процентов. На сколько процентов увеличилось производство валовой продукции в каждой из отраслей?

3. За счет снижения спроса производство конечной продукции первой отрасли сократилось вдвое. На сколько процентов сократится производство валовой продукции в каждой из отраслей?

Решение:

1. Определить величину валовой продукции для каждой отрасли и заполнить балансовую таблицу.

Составим матрицу прямых затрат (технологическую матрицу)

,

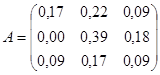где аij - коэффициенты прямых затрат

и вектор конечной продукции

,

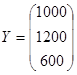где yi -конечный продукт i-ой отрасли, i = 1,2… n

Для расчета величины валовой продукции каждой отрасли составим систему уравнений Леонтьева:

,

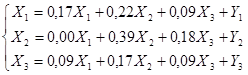где Xi - валовая продукция i-ой отрасли, i= 1,2….n

Введем вектор X = (X1,X2,X3) и Y = (Y1,Y2,Y3)

Из системы уравнений Леонтьева

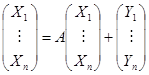
получаем уравнение Леонтьева в матричной форме

решением которого является

Для нахождения Xi нам потребуется единичная матрица:

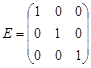
Составим матрицу (E- A)

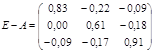
Для того, чтобы проверить, существует ли матрица, обратная матрице (E-A), вычислим ее определитель

det(E-A) = 0,4268

Так как определитель матрицы (E-A) не равен 0, значит, она имеет обратную. Для нахождения обратной матрицы составим алгебраические дополнения.

Теперь составим матрицу B, обратную матрице (E - A)

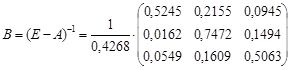
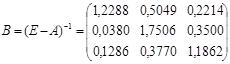
- матрица полных затрат, где bij - коэффициенты полных затрат.

Чтобы определить, верны ли вычисления, необходимо проверить следующее равенство:

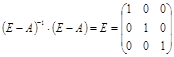
Равенство выполняется, значит, расчеты верны.

Составим систему линейных равенств

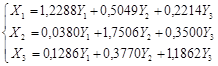
Найдем вектор X = (X1,X2,X3)

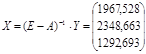
По формуле (где aij - количество продукции i - ой отрасли, необходимой для производства ед. валовой продукции j - ой отрасли) определим Xij- количество продукции i-ой отрасли, которое используется в j-ой отрасли в качестве материальных затрат.

Составляем балансовую таблицу

 Скачать реферат