Моделирование экономики
Аганбегян Абел Газевич ( р. 1932 г. ), академик, основные труды по проблемам производительности труда, отраслевой оптимизации.
Фельдман Григорий Александрович ( 1884 – 1958 г.г. ), советский экономист, создал первую динамическую модель экономического роста.
Федоренко Николай Прокофьевич ( р. 1917 г. ) академик, советский экономист, организатор и директор ЦЭМИ до 1985 года, работал в обл
асти общих проблем применения ЭММ в народном хозяйстве.
ЛЕКЦИЯ 2
Тема: Классификация ЭММ и моделей
План
Классификационная схема ЭММ и моделей
Понятие модели, виды моделей
ЭМ методы – обобщающее название дисциплин, находящихся на стыке экономики, математики и кибернетики, введенное В. С. Немчиновым в начале 60-х годов 20 в. Общепринятой классификации ЭММ и моделей нет, на рис. 2.1
Приведена примерная классификация ЭММ и моделей.
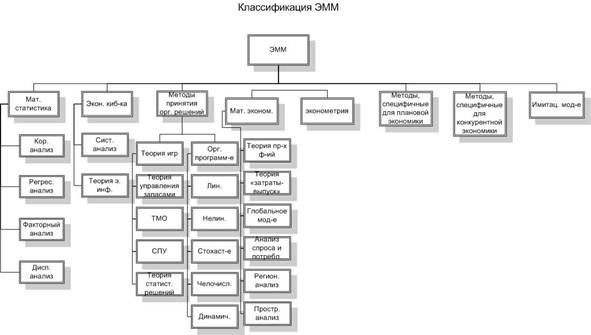
Рис. 2.1
Рассмотрим схему ЭММ и моделей:
1. Математическая статистика – раздел прикладной математики, основанный на выборке изучаемых явлений.
2. Математическая экономика и эконометрия – науки, занимающиеся проверкой экономических теорий на фактическом материале с использованием математической статистики и математических моделей.
Эконометрия – наука изучающая конкретные количественные закономерности и взаимосвязи экономических объектов и процессов с помощью математических и математико-статических методов и моделей.
Математическая экономика – наука, изучающая те же вопросы, что и эконометрия, только без статистической конкретизации экономических параметров, в виде общих экономических зависимостей.
Математической экономикой – называют прикладную часть математической экономики.
Производственные функции – ЭМ уравнения связывающие переменные величины затрат с величинами продукции, применяется в макроэкономических расчетах и на уровне предприятий.
Межотраслевой баланс – каркасная модель экономической таблицы, в которой показываются многообразные натуральные и стоимостные связи в народном хозяйстве ( за рубежом называют методом « затраты - выпуск » ).
Теория экономического роста – позволяет моделировать общее и социальное развитие стран в целом.
Региональный анализ – исследует уровни экономического развития регионов, их специализации, отраслевые структуры.
Пространственный анализ – исследует размещение населенных центров в связи с их экономическим значением, сферой сбыта продукции. Отрасли делятся на пространствоемкие ( сельское хозяйство, рыболовство ), точечные ( обрабатывающая промышленность ), сокращающая расстояние ( транспорт и связь ).
3. Экономическая кибернетика рассматривает применение общих законов кибернетики в изучении экономических явлений ( системный анализ экономики, теория экономической информации ).
Системный анализ экономики – рассматривает экономические объекты как систему, главный инструмент – модель изучаемой системы.
Теория экономической информации - рассматривает процессы происходящие в экономике, только с информационной стороны, рационализацию потоков экономической информации, ее полезность.
4. Методы принятия оптимальных решений ( теория игр, массового обслуживания, управления запасами и др.).
2. Модель – понятие, которое определить трудно. В одной работе было перечислено 31 определение. Это понятие знакомо каждому : игрушечный самолет – модель самолета. Фотоснимок пейзажа – это модель местности,
s = vt ( путь = скорость * на время, модель движущегося тела, математическая модель ).
Модели могут быть более или менее точные, более или менее простые или сложные, материальные ( вещественные ) и знаковые ( например, графические ).
Материальные модели – модели гидроэлектростанций, воспроизводящие реку, горы ;
Термин «модель» происходит от латинского слова «modulus» - образец Моделью некоторого объекта, явления называется исскуственная система или объект, которые в определенных условиях могут заменить оригинал путем воспроизведения свойств и характеристик оригинала.
Модель есть вспомогательным средством, которое в определенной ситуации заменяет оригинал при исследовании его свойств. Различают модели следующих видов
1) физические ( внешнего подобия ),
2) схематические ( графические ),
3) словесные ( вербальные ),
4) математические.
Математические модели являются наиболее абстрактными.
Под ЭМ моделями понимаются математические модели, применяемые для решения экономических задач и описания экономических процессов или явлений. ЭМ модели бывают
1 теоретико-аналитические и прикладные,
2 общие и частные,
3 непрерывные и дискретные,
4 статические и динамические,
5 детерминированные и стохастические,
6 матричные и др.
Большое значение в экономики имеют оптимизационные модели. Они состоят из целевой функции или критерия оптимальности и ограничений.
Целевая функция – ( или функция цели, название оптимизируемой функции ) – функция, оптимум которой требуется найти
ƒ ( х ) ![]() opt (max, min).
opt (max, min).
Критерий оптимальности – признак, характеризующий качество принимаемого решения.
К = opt ƒ ( х ), x є X.
Ограничения выражаются равенствами и неравенствами
F1( х ) > A,
F2( х ) = В.,
Важное свойство ЭМ моделей – их применимость к разным
ситуациям. Например выпуск продукции и внесение удобрений можно описать одинаковой моделью.
Лекция 3 Тема: Этапы экономико - математическогомоделирования
План
1. Анализ этапов экономико-математического моделирования.
2. Вербально-информационное описание как начальный этап моделирования.
3. Модели мировой динамики.
1. Процесс моделирования, в том числе и экономико-математического, включает в себя три структурных элемента: объект исследования; субъект (исследователь); модель, опосредующую отношения между познающим субъектом и познаваемым объектом. Рассмотрим общую схему процесса моделирования, состоящую из четырех этапов.
Пусть имеется некоторый объект, который мы хотим исследовать методом моделирования. На первом этапе мы конструируем (или находим в реальном мире) другой объект – модель исходного объекта-оригинала. Этап построения модели предполагает наличие определенных сведений об объекте-оригинале. Познавательные возможности модели определяются тем, что модель отображает лишь некоторые существенные черты исходного объекта, поэтому любая модель замещает оригинал в строго ограниченном смысле. Из этого следует, что для одного объекта может быть построено несколько моделей, отражающих определенные стороны исследуемого объекта или характеризующих его с разной степенью детализации.
На втором этапе процесса моделирования модель выступает как самостоятельный объект исследования.
На пример, одну из форм такого исследования составляет проведение модельных экспериментов, при которых целенаправленно изменяются условия функционирования модели и систематизируются данные о ее поведении. Конечным результатом этого этапа является совокупность знаний о модели в отношении существенных сторон объекта-оригинала, которые отражены в данной модели. Третий этап заключается в переносе знаний с модели на оригинал, в результате чего мы формируем множество знаний об исходном объекте и при этом переходим с языка модели на язык оригинала. С достаточным основанием переносить какой-либо результат с модели на оригинал можно лишь в том случае, если этот результат соответствует признакам сходства оригинала и модели (другими словами, признакам адекватности).
Другие рефераты на тему «Экономико-математическое моделирование»:
Поиск рефератов
Последние рефераты раздела
- Выборочные исследования в эконометрике
- Временные характеристики и функция времени. Графическое представление частотных характеристик
- Автоматизированный априорный анализ статистической совокупности в среде MS Excel
- Биматричные игры. Поиск равновесных ситуаций
- Анализ рядов распределения
- Анализ состояния финансовых рынков на основе методов нелинейной динамики
- Безработица - основные определения и измерение. Потоки, запасы, утечки, инъекции в модели
