Моделирование экономики
![]() ,
,
![]() ,
,
![]() .
.
Параметры ![]() и
и ![]() выражают эластичность уровня производства
выражают эластичность уровня производства width=16 height=21 src="images/referats/9813/image047.png">по отношению к факторам
![]() и
и ![]() , то есть показывают относительный прирост продукции, связанный с относительным приростом
, то есть показывают относительный прирост продукции, связанный с относительным приростом ![]() и
и ![]() .
.
![]() - объем трудовых ресурсов в натуральном количестве,
- объем трудовых ресурсов в натуральном количестве,
![]() - число рабочих, число человеко-дней,
- число рабочих, число человеко-дней,
![]() - выпуск продукции в стоимостном или натуральном виде.
- выпуск продукции в стоимостном или натуральном виде.
в) более сложные производственные функции CES
![]() ,
,
где ![]() - параметр, выражающий эластичность замены ОФ и занятости.
- параметр, выражающий эластичность замены ОФ и занятости.
2. Предполагается, что производственные факторы удовлетворяют аксиоме. Существует подмножество производства страны затрат, называемое экономической областью ![]() , в которой увеличение любого вида затрат не приводит к уменьшению выпуска. Если
, в которой увеличение любого вида затрат не приводит к уменьшению выпуска. Если ![]() - две точки этой области, то
- две точки этой области, то ![]() влечет
влечет ![]() .
.
Эта аксиома утверждает, что производственные факторы не какая-то совершенно абстрактная функция, придуманная теоретиками - математиками.
Она отражает утверждение, пусть и не на всей своей области определения, а только на ее части: в мало-мальски разумной экономике увеличение затрат не может привести к уменьшению выпуска.
В дифференциальной форме это выражается в том, что в этой области первые частные производные функции неотрицательны: ![]() - непрерывная и дифференцируемая
- непрерывная и дифференцируемая
![]() .
.
![]() .
.
Эти производные называются предельными продуктами.
Можно составить производственные функции данного производства даже ничего не зная о производстве. Надо только поставить у возможного производства счетчик (человека на какое-то автоматическое увеличение), который будет фиксировать увеличиваемые ресурсы и ![]() - количество продукции, которую производство произвело. Если накопить достаточно много такой статической информации, учесть работу производства в различных режимах, то можно прогнозировать выпуск продукции, зная объем ввезенных ресурсов, а это и есть производственная функция.
- количество продукции, которую производство произвело. Если накопить достаточно много такой статической информации, учесть работу производства в различных режимах, то можно прогнозировать выпуск продукции, зная объем ввезенных ресурсов, а это и есть производственная функция.
3 Понятие «однородность производственной функции» включает в себя следующее ее свойство: равномерное увеличение всех производственных факторов вызывает пропорциональное увеличение продукта. Выразим это математически:
Функция ![]() однородна в степени h. если
однородна в степени h. если
![]() .
.
Таким образом, когда каждая независимая переменная принимает значения ![]() , значение функции
, значение функции ![]() возрастает в
возрастает в ![]() раз.
раз.
Величина ![]() показывает степень использования производственных факторов или их эффективность. В случае, когда
показывает степень использования производственных факторов или их эффективность. В случае, когда ![]() , эффективность производственных факторов будет равна 1, при
, эффективность производственных факторов будет равна 1, при ![]() говорят, что производственные факторы обладают растущей эффективностью и соответственно при
говорят, что производственные факторы обладают растущей эффективностью и соответственно при ![]() эффективность факторов снижается
эффективность факторов снижается
4. Эластичностью экономического показателя называется его способность реагировать в большей или меньшей степени на изменение другого показателя.
Определим эластичность объема производства ![]() по некоторому фактору как отношение темпов прироста
по некоторому фактору как отношение темпов прироста ![]() к темпам прироста этого фактора.
к темпам прироста этого фактора.
Рассчитаем коэффициент эластичности ![]() по основным фондам
по основным фондам ![]() :
:
![]() ;
;
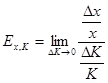 ;
;
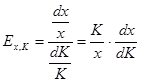 ;
;
Здесь ![]() - непрерывная дифференцируемая функция по
- непрерывная дифференцируемая функция по ![]() .
.
Так как на практике это условие выполняется редко, то коэффициент эластичностьи часто выражается через приросты.
![]() ;
;
Пусть ![]() , тогда
, тогда
![]() - равен относительному изменению
- равен относительному изменению ![]() .
.
![]() ;
;
Коэффициент эластичности показывает как изменяется (в %) величина ![]() , если величина
, если величина ![]() возрастает на 1%.
возрастает на 1%.
Если коэффициент эластичности в какой-нибудь точке равен 1, то относительная и предельная величины равны друг другу. Это выполняется в точках, в которых относительная величина достигает минимума или максимума.
Иногда экономические показатели характеризуются коэффициентом эластичности. Если ![]() , то говорят, что экономический показатель эластичен по
, то говорят, что экономический показатель эластичен по ![]() ; если
; если ![]() , то говорят, что экономический показатель абсолютно эластичен.
, то говорят, что экономический показатель абсолютно эластичен.
Так как производственная функция содержит несколько факторов, то следует исследовать эластичность по всем факторам. Вводится понятие частной эластичности.
Другие рефераты на тему «Экономико-математическое моделирование»:
- Линейное программирование
- Сущность, модели, границы применения метода производственной функции
- Макроэкономическая статистика
- Взаимозаменяемость продовольственных продуктов - масла животного и масла растительного. Их потребление
- Пакет программ Майкрософт, как эффективное средство эконометрического анализа
Поиск рефератов
Последние рефераты раздела
- Выборочные исследования в эконометрике
- Временные характеристики и функция времени. Графическое представление частотных характеристик
- Автоматизированный априорный анализ статистической совокупности в среде MS Excel
- Биматричные игры. Поиск равновесных ситуаций
- Анализ рядов распределения
- Анализ состояния финансовых рынков на основе методов нелинейной динамики
- Безработица - основные определения и измерение. Потоки, запасы, утечки, инъекции в модели
