Линейное программирование как метод оптимизации

X1 + X2 + X3 + 2X4 ≤ 3

X1 + 2X2 + 3X3 + X4 ≤ 7

X1, X2, X3, X4 ≥ 0

Составим двойственную задачу по следующей схеме:

число переменных в дв. задаче равно числу ограничений в исходной, а число ограничений в дв. равно числу переменных в исходной;

в дв. задаче меняется вид экстремума (min→max);

векторы правой части и коэффициентов целевой функции в дв

. задаче меняются местами: первый становится вектором коэффициентов целевой функции, а второй - вектором правой части в системе ограничений;

левая часть системы ограничений строится по транспонированной матрице (строки меняются со столбцами), которая умножается на вектор переменных двойственной задачи

знаки в системе ограничений двойственной задачи определяются знаками ограничений неотрицательности в исходной задаче.

g = 3Y1+7Y2 → min

Y1 + Y2 ≥ 9

Y1 + 2Y2 ≥ 14

Y1 + 3Y2 ≥ 15

2Y1 + Y2 ≥ 10

Y1, Y2 ≥ 0

б) Решим задачу графическим методом

в) Оптимальным планом задачи 2, решенной симплексным методом является:

Х2 = (0,2,1,0,0,0); F2 = 9*0+14*2+15*1+0 = 43

Используя 3 симплексную таблицу найдем оптимальный план двойственной задачи.

Из 1 теоремы двойственности следует что: Y=Cб*А - 1

Составим матрицу А из компонентов векторов входящих в оптимальный базис

А = Р2; Р3 =

Определим обратную матрицу А-1:

А-1 =Р5; Р6= = (12;

1)

Оптимальный план двойственности равен:

Y = (12, 1, 0, 0, 0, 0); G = 3*12+7*1 = 43

Подставим оптимальный план прямой задачи в систему ограничений

12+1 > 9

12+2*1 = 14

12+3*1 = 15

2*12+1 > 10

Первое ограничение двойственной задачи выполняется как строгое неравенство. Это означает, что двойственная оценка сырья, используемого на производство одного изделия 1 и 4 вида, выше цены этого изделия и, следовательно, выпускать изделия этих видов невыгодно. Его производство и не предусмотрено оптимальным планом прямой задачи. Второе и третье ограничения двойственной задачи выполняются как строгие равенства. Это означает, что двойственные оценки сырья, используемого для производства единицы соответственно изделий 2 и 3 вида, равны в точности их ценам. Поэтому выпускать эти два вида продукции по двойственным оценкам экономически целесообразно. Их производство и предусмотрено оптимальным планом прямой задачи.

Таким образом, двойственные оценки тесным образом связаны с оптимальным планом прямой задачи. Всякое изменение исходных данных прямой задачи может оказать влияние как на ее оптимальный план, так и на систему оптимальных двойственных оценок. Поэтому, чтобы проводить экономический анализ с использованием двойственных оценок, нужно знать их интервал устойчивости. К рассмотрению этого мы сейчас и перейдем.

Таким образом, получим тот же результат, который приведен в симплекс-таблице для оптимального решения прямой задачи.

Анализ сопоставления результатов, полученных при решении прямой и двойственной задачи, позволяет сформулировать интересный вывод.

На итерации, приводящей к оптимуму, Это равенство справедливо всегда и фактически соответствует оптимальным значениям переменных обеих задач.

Основная и двойственная к ней задачи образуют пару взаимно двойственных задач: двойственная задача к двойственной оказывается основной задачей. Т.е. если мы возьмем двойственную задачу и по теоремам двойственности перейдем ко второй двойственной задаче она окажется прямой задачей.

используя вторую теорему двойственности, найти решение исходной.

Значение линейной функции двойственной задачи от Y численно равно минимальному значению линейной функции исходной задачи

Пропустим процесс решения двойственной ЗЛП, записав только результаты:

Y1=12 Y2=1 Y3=0 min (φ) =43

Т.к max (f) =min (φ), решение исходной задачи уже известно. Остаётся только найти значения X1, X2, X3, при которых это значение достигается. Здесь мы применим вторую теорему двойственности, которая устанавливает следующее соответствие:

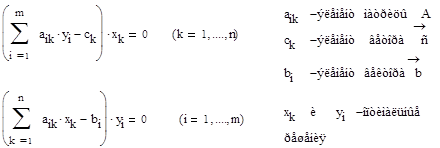
В нашем примере получается следующая система линейных уравнений:

Y1 + Y2 = 9

Y1 + 2Y2 = 14

Y1 + 3Y2 = 15

2Y1 + Y2 = 10

С= (3,7) y1=12 y2=1 т.к. у1>0 и y2>0, то

X1 + X2 + X3 + 2X4 =3

X1 + 2X2 + 3X3 + X4 =7

12+1≠ 9, х1=0

12+2*1=14 → х2≠ 0

12+3*1=15→ х3≠ 0

2*12+1≠10, х4=0

х2+х3=3 Х2*=2

2х2+3х3=7 Х3*=1

F = 9*0+14*2+15*1+0 = 43

6. Транспортная задача и её решение методом потенциалов

Исходные данные приведены в таблице 3, найти оптимальный план.

Таблица 3.

 Скачать реферат