Коэффициент детерминации. Значимость уравнения регрессии

Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, т.к. >.

Средняя относительная ошибка аппроксимации находится по формуле:

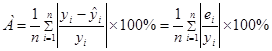
Таблица 7. Промежуточные вычисления для рас

чета средней относительной ошибки аппроксимации.

,

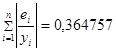
значит модель имеет хорошее качество.

Рассчитаем коэффициент эластичности по формуле:

6. осуществить прогнозирование среднего значения показателя Y при уровне значимости , если прогнозное значение фактора X составит 80% от его максимального значения.

Рассчитаем стандартную ошибку прогноза

,

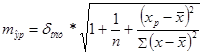где

=930,4 ;

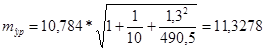
, для уровня значимости 0,1 и числа степеней свободы n-2=8

Доверительный интервал прогноза:

Таким образом, =61,112 , будет находиться между верхней границей, равной 82,176 и нижней границей, равной 40,048.

7. Представить графически фактические и модельные значения Y точки прогноза.

Воспользуемся данными из таблицы 2 для построения графиков с помощью MS Excel.

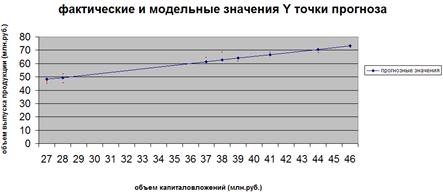
Рис. 2. Фактические и модельные значения Y точки прогноза.

8. Составить уравнения нелинейной регрессии: гиперболической, степенной, показательной. Привести графики построенных уравнений регрессии.

Построение степенной модели.

Уравнение степенной модели имеет вид:

Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения:

Обозначим .

Тогда уравнение примет вид – линейное уравнение регрессии. Рассчитаем его параметры, используя данные таблицы 1:

Таблица 8. Расчет параметров уравнения степенной модели регрессии.

 Скачать реферат