Понятие о физической величине. Международная система единиц физических величин СИ

Наиболее просто производится интерполирование, когда интервалы между значениями аргумента постоянны, т. е.

, (7.2)

где h – постоянная величина, называемая шагом. В общем случае

. (7.3)

При использовании интерполяционных формул приходится иметь дело с

разностями значений у и разностями этих разностей, т. е. разностями функции у(х) различных порядков. Разности любого порядка вычисляются по формуле

. (7.4)

Например,

и .

При вычислении разностей их удобно располагать в виде таблицы (см. Табл. 4), в каждом столбце которой разности записывают между соответствующими значениями уменьшаемого и вычитаемого, т. е. составляется таблица диагонального типа. Обычно разности записывают в единицах последнего знака.

Таблица 4

Разности функции у(х)

Так как функция у(х) выражается многочленом (7.1) n-ой степени относительно х, то разности также являются многочленами, степени которых понижаются на единицу при переходе к последующей разности. N-я разность многочлена n-ой степени является постоянным числом, т. е. содержит х в нулевой степени. Все разности более высокого порядка равны нулю. Это определяет степень интерполирующего многочлена.

Преобразовав функцию (7.1), можно получить первую интерполяционную формулу Ньютона:

. (7.5)

Она используется для нахождения значений у при любых х в пределах измерений. Представим эту формулу (7.5) в несколько ином виде:

. (7.6)

Последние две формулы иногда называют интерполяционными формулами Ньютона для интерполирования вперед. В эти формулы входят разности, идущие по диагонали вниз, и их удобно использовать в начале таблицы экспериментальных данных, где разностей достаточно.

Вторая интерполяционная формула Ньютона, выведенная из того же уравнения (7.1), выглядит следующим образом:

. (7.7)

Данную формулу (7.7) принято называть интерполяционной формулой Ньютона для интерполирования назад. Она используется для определения значений у в конце таблицы.

Теперь рассмотрим интерполяцию при неравноотстоящих значениях аргумента.

Пусть по-прежнему функция у(х) задается рядом значений хi и уi, но интервалы между последовательными значениями хi неодинаковы. Использовать вышеприведенные формулы Ньютона нельзя, так как они содержат постоянный шаг h. В задачах такого рода необходимо вычислить приведенные разности:

; и т. д.

; и т. д. (7.8)

Разности более высоких порядков вычисляются аналогично. Как и для случая равноотстоящих значений аргумента, если f(х) – многочлен n-ой степени, то разности n-го порядка постоянны, а разности более высокого порядка равны нулю. В простых случаях таблицы приведенных разностей имеют вид, аналогичный таблицам разностей при равноотстоящих значениях аргумента.

Помимо рассмотренных интерполяционных формул Ньютона часто применяют интерполяционную формулу Лагранжа:

. (7.9)

В этой формуле каждое из слагаемых представляет собой многочлен n-ой степени и все они равноправны. Поэтому до окончания вычислений нельзя пренебрегать какими-либо из них.

Обратное интерполирование. На практике иногда бывает необходимо найти значение аргумента, которому соответствует определенное значение функции. В этом случае интерполируют обратную функцию и следует иметь в виду, что разности функции не постоянны и интерполирование нужно проводить для неравноотстоящих значений аргумента, т. е. использовать формулу (7.8) или (7.9).

Экстраполирование. Экстраполированием называют вычисление значений функции у за пределами интервала значений аргумента х, в котором были проведены измерения. При неизвестном аналитическом выражении искомой функции экстраполирование нужно проводить весьма осторожно, так как не известно поведение функции у(х) за пределами интервала измерений. Экстраполяция допускается, если ход кривой плавный и нет причин ждать резких изменений в исследуемом процессе. Тем не менее экстраполирование должно проводиться в узких пределах, например в пределах шага h. В более далеких точках можно получить неверные значения у. Для экстраполирования применяются те же формулы, что и для интерполирования. Так, первая формула Ньютона используется при экстраполировании назад, а вторая формула Ньютона – при экстраполировании вперед. Формула Лагранжа применяется в обоих случаях. Надо также иметь в виду, что экстраполирование приводит к большим погрешностям, чем интерполирование.

Численное интегрирование.

Формула трапеций. Формулу трапеций обычно применяют в том случае, если значения функции измерены для равноотстоящих значений аргумента, т. е. с постоянным шагом. По правилу трапеций в качестве приближенного значения интеграла

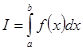(7.10)

принимают величину

, (7.11)

 Скачать реферат