Транспортная задача с ограничениями возможных транспортных средств

Если экономико-математическая модель задачи линейна, то оптимальный план достигается в крайней точке области изменения переменных величин системы ограничений. В случае нелинейной модели оптимальных планов и оптимальных значений целевой функции может быть несколько. Поэтому необходимо определять экстремальные планы и экстремальные значения целевой функции. План, для которого целевая функция моде

ли имеет экстремальное значение, называют экстремальным планом, или экстремальным решением.

Для нелинейных моделей иногда существуют экстремальные значения целевой функции, а для линейных моделей экстремальных планов и экстремальных значений целевой функции быть не может.

Таким образом, для принятия оптимального решения любой экономической задачи необходимо построить ее экономико-математическую модель, по структуре включающую в себе систему ограничений, целевую функцию, критерий оптимальности и решение.

Методика построения экономико-математической модели состоит в том, чтобы экономическую сущность задачи представить математически, используя различные символы, переменные и постоянные величины, индексы и другие обозначения. Все условия задачи необходимо записать в виде уравнений или неравенств. Поэтому, в первую очередь необходимо определить систему переменных величин, которые могут для конкретной задачи обозначить искомый объем производства продукции на предприятии, количество перевозимого груза поставщиками конкретным потребителям.

1.4 Математическая постановка задачи

Математическая модель транспортной задачи в общем случае имеет вид

(1.1)

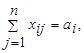i=1,2,…,m, (1.2)

j=1,2,…,n, (1.3)

i=1,2,…,m; j=1,2,…,n. (1.4)

Целевая функция задачи (1.1) выражает требования обеспечить минимум суммарных затрат на перевозку всех грузов. Первая группа из т уравнений (1.2) описывает тот факт, что запасы всех т поставщиков вывозятся полностью. Вторая группа из n уравнений (1.3) выражает требования полностью удовлетворить запросы всех n потребителей. Неравенства (1.4) являются условиями неотрицательности всех переменных задачи.

Таким образом, математическая формулировка транспортной задачи состоит в следующем: найти переменные задачи

i=1,2,…,m; j=1,2,…,n, (1.5)

удовлетворяющее системе ограничений (1.2), (1.3), условиям неотрицательности (1.4) и обеспечивающее минимум целевой функции (1.1).

В рассмотренной модели транспортной задачи предполагается, что суммарные запасы поставщиков равны суммарным запросам потребителей, т.е.

. (1.6)

1.5 Транспортная задача с ограниченными возможностями транспортных средств

Под названием “транспортная задача” объединяется широкий круг задач с единой математической моделью. Данные задачи относятся к задачам линейного программирования и могут быть решены симплексным методом. Однако матрица системы ограничений транспортной задачи настолько своеобразна, что для ее решения разработаны специальные методы. Эти методы, как и симплексный метод, позволяют найти начальное опорное решение, а затем, улучшая его, получить оптимальное решение.

В общей постановке транспортной задачи предполагается, что из любого пункта производства любой пункт потребления может быть перевезено любое количество груза.

В целом ряде случаев оптимизации планирования перевозок приходится учитывать ограниченные возможности транспортных путей и средств. Поэтому математическую модель транспортной задачи:

(1.7)

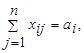i=1,2,…,m, (1.8)

j=1,2,…,n, (1.9)

(1.10)

должны быть введены дополнительные ограничительные условия, учитывающие возможность транспортных путей и средств.

Если обозначиться транспортные возможности между пунктами I и j через dij, то количество груза , которое может быть перевезено по этому направлению за планируемый период времени, не должно превышать транспортных возможностей, т.е.

(1.11)

Тогда ограничения 1.10, 1.11 объединяются, и модель задачи усложняется двусторонними ограничениями на переменные

(1.12)

При этом общая транспортная возможность дорог, соединяющих I -й пункт производства со всеми n пунктами потребления, должна быть ровна или больше количества продукции, предназначенной к постановке из этого i-го пункта всем n потребителя, т.е.

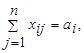i=1,2,…,m, (1.13)

Общая же транспортная возможность дорог, соединяющих j-й пункт потребления со всеми m пунктами производства, должна быть равна или больше количества продукции, которые надо поставить в этот j-й пункт от всех m поставщиков, т.е.

i=1,2,…,n, (1.14)

Существуют различные подходы к решению этой задачи. Рассмотрим наиболее простой из них.

Путей некоторых преобразований условий ее можно свести к типу обычной транспортной задачи. Для этого пункт производства или потребления, для которых условия ограничены транспортные возможности, разбивается на два условных пункта. При этом следует подчеркнуть непременно один пункт.

Мощность условного поставщика А’i - принимается равный установленной возможности средств, соединяющих пункт и с потребителями j

A’i=dij (1.15)

а мощность условного поставщика А’j - равной разности между заданными в условии задачи мощностью поставщика в пункте I и возможностью средств между I-м и j-м пунктами, т.е.

a’’i=ai-dij. (1.16)

При этом затраты на поставку грузов из пунктов I’ в пункт j-cij принимаются равными действительным расходам cij приведенным в условии задачи. В оптимальном решение переменные хij могут иметь любое неотрицательное значение от нуля до a’i, т.е.

(1.17)

В отличие от них переменные хij в оптимальном решении непременно должны быть равны нулю, поскольку мощность А’j характеризует количество в пункте и сверх установленной средств, соединяющих пункты i и j, следовательно это часть груза должна быть направлена не j-му а любому другому потребителю. Для того, чтобы в оптимальном решении обеспечить значение переменных хij равно нулю, затраты на поставку груза из пункта i’’ в пункт j принимаются равными М, т. е cij=М.

При минимизации целевой функции (1.7) и коэффициентах cij=М, в оптимальном решении получим

 Скачать реферат